科普介紹

帶電荷 \(q\) 的粒子波函數 \(\Psi\) 滿足薛丁格方程式： \[ i\hbar \partial_t \Psi = \frac{\hat{p}^2}{2m} \Psi + V\Psi, \] 其中動量算符 \(\hat{p}\) 在電磁勢 \((\phi, \mathbf{A})\) 的作用下，表達為（SI 單位）： \[ \hat{p} = \frac{\hbar}{i} \nabla - q\mathbf{A}. \] 將其代入薛丁格方程式，我們得到： \[ i\hbar \partial_t \Psi = \frac{1}{2m} \left( \frac{\hbar}{i} \nabla - q\mathbf{A} \right) \left( \frac{\hbar}{i} \nabla \Psi - q\mathbf{A}\Psi \right) + V\Psi. \] 展開後為： \[ i\hbar \partial_t \Psi = -\frac{\hbar^2}{2m} \nabla^2 \Psi - \frac{q}{2m} \frac{\hbar}{i} \nabla \cdot (\mathbf{A}\Psi) - \frac{q}{2m} \frac{\hbar}{i} \mathbf{A} \cdot \nabla \Psi + \frac{q^2 A^2}{2m} \Psi + \phi\Psi. \]

共軛方程為： \[ -i\hbar \partial_t \Psi^* = -\frac{\hbar^2}{2m} \nabla^2 \Psi^* + \frac{q}{2m} \frac{\hbar}{i} \nabla \cdot (\mathbf{A} \Psi^*) + \frac{q}{2m} \frac{\hbar}{i} \mathbf{A} \cdot \nabla \Psi^* + \frac{q^2 A^2}{2m} \Psi^* + \phi \Psi^*. \]

將兩式分別乘以 \(\Psi^*\) 和 \(\Psi\)，再相減，得到： \[ i\hbar (\Psi^* \partial_t \Psi + \Psi \partial_t \Psi^*) = -\frac{\hbar^2}{2m} (\Psi^* \nabla^2 \Psi - \Psi \nabla^2 \Psi^*) - \frac{q}{2m} \frac{\hbar}{i} \left[ \Psi^* \nabla \cdot (\mathbf{A}\Psi) + \Psi \nabla \cdot (\mathbf{A}\Psi^*) + \Psi^* \mathbf{A} \cdot \nabla \Psi + \Psi \mathbf{A} \cdot \nabla \Psi^* \right]. \] 簡化後得到： \[ i\hbar \partial_t (\Psi^* \Psi) = -\frac{\hbar^2}{2m} \nabla \cdot (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q}{2m} \frac{\hbar}{i} \nabla \cdot (2\mathbf{A} \Psi^* \Psi). \]

除以 \(i\hbar\)，得： \[ \partial_t (\Psi^* \Psi) = -\nabla \cdot \left[ \frac{\hbar}{2mi} (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q\mathbf{A}}{m} \Psi^* \Psi \right]. \] 比較連續性方程式： \[ \partial_t \rho + \nabla \cdot \mathbf{J} = 0, \] 其中 \(\rho = \Psi^* \Psi\) 為機率密度，可得機率流： \[ \mathbf{J} = \frac{\hbar}{2mi} (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q\mathbf{A}}{m} \Psi^* \Psi. \]

對於帶電粒子，其電流密度 \(\mathbf{J}_q\) 為： \[ \mathbf{J}_q = q \mathbf{J} = q \left[ \frac{\hbar}{2mi} (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q\mathbf{A}}{m} \Psi^* \Psi \right]. \] 若波函數以粒子密度 \(n(\mathbf{r})\) 和相位 \(\theta(\mathbf{r})\) 表示，即 \(\Psi \sim \sqrt{n(\mathbf{r})} e^{i\theta(\mathbf{r})}\)，則有： \[ \mathbf{J}_q = q\frac{\hbar}{m} n(\mathbf{r}) \left[ \nabla \theta(\mathbf{r}) - \frac{q\mathbf{A}}{\hbar} \right]. \]

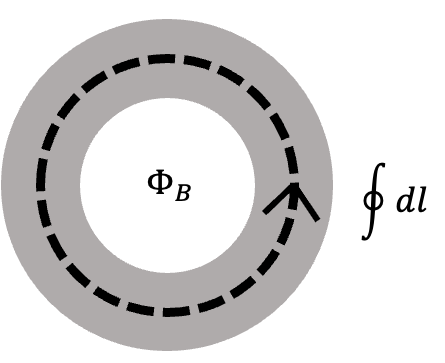
在拓樸條件下，根據斯托克斯定理： \[ \int \nabla \times \left[ \nabla \theta(\mathbf{r}) - \frac{q\mathbf{A}}{\hbar} \right] \cdot d\mathbf{S} = \int \nabla \times (\nabla \theta(\mathbf{r})) \cdot d\mathbf{S} - \frac{q}{\hbar} \int (\nabla \times \mathbf{A}) \cdot d\mathbf{S}, \] 簡化為： \[ \oint \nabla \theta(\mathbf{r}) \cdot d\mathbf{l} - \frac{q}{\hbar} \Phi_B = \begin{cases} 0, & \text{若環路無孔洞}, \\ 2\pi N, & \text{若環路有孔洞}. \end{cases} \]