科普介紹

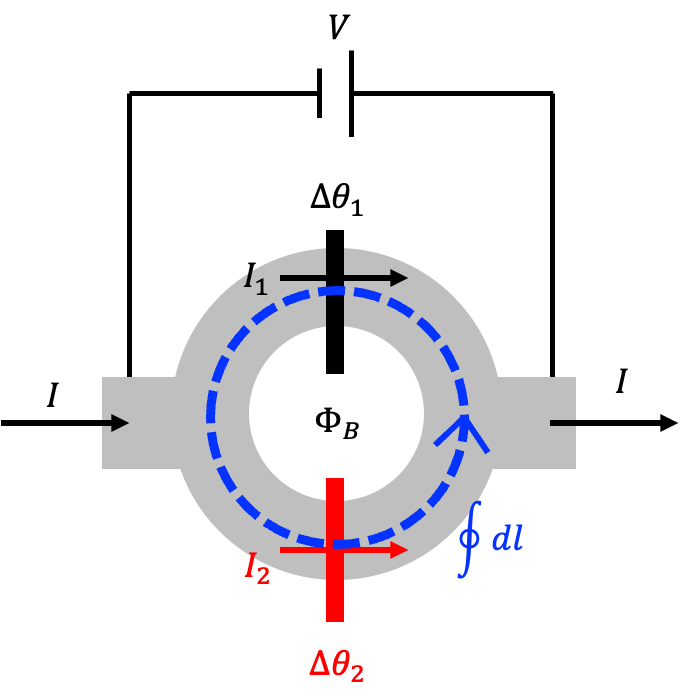
將兩組約瑟夫森節 \(J_1\)、\(J_2\) 相組，中間形成一個閉環，通入磁通 \( \Phi_B \) 與電壓 \( V \)。在前一節中，超導函數的相位對閉環的積分需滿足： \[ \oint \nabla \theta(r) \cdot d\vec{l} - \frac{q}{\hbar} \Phi_B = 2\pi N \] 因為在接面不連續會貢獻 \( \Delta\theta_1 \)、\( \Delta\theta_2 \)，\( q = -2e \)，帶入得： \[ \Delta\theta_2 - \Delta\theta_1 + 2\pi \frac{\Phi_B}{\Phi_0} = 2\pi N \] \[ \Delta\theta_2 = \Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0} + 2\pi N \]

當整個 SQUID 通入電流 \( I = I_1 + I_2 \)，並使用前一節約瑟夫森節電流的關係式（這裡考慮對稱的 SQUID，即兩個約瑟夫森節的特性 \( I_c \) 相同），計算得： \[ I = I_1 + I_2 = I_0 (\sin\Delta\theta_1 + \sin\Delta\theta_2) \] \[ I = I_0 \left[\sin\Delta\theta_1 + \sin\left(\Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0} + 2\pi N\right)\right] \] \[ I = I_0 \left[\sin\Delta\theta_1 + \sin\left(\Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0}\right)\right] \] 利用三角恆等式化簡： \[ I = I_0 \left[2 \sin\left(\frac{\Delta\theta_1 + \Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0}}{2}\right) \cos\left(\frac{\Delta\theta_1 - \Delta\theta_1 + 2\pi \frac{\Phi_B}{\Phi_0}}{2}\right)\right] \] \[ I = 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \sin\left(\Delta\theta_1 - \frac{\Phi_B}{\Phi_0} \pi\right) \]

前一節提到約瑟夫森節具有電感的性質，同理我們可以討論 SQUID 的電感性質。將電流對時間微分： \[ \dot{I} = 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \cos\left(\Delta\theta_1 - \frac{\Phi_B}{\Phi_0} \pi\right) \dot{\Delta\theta_1} \] 而 \( \dot{\Delta\theta_1} \) 與電壓 \( V \) 的關係為： \[ V = \frac{\hbar}{2e} \dot{\Delta\theta_1} = \frac{\Phi_0}{2\pi} \dot{\Delta\theta_1} \] 帶入後可得電感值： \[ L_{\text{SQUID}}(\Delta\theta_1, \Phi_B) = \left[\frac{2\pi}{\Phi_0} \cdot 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \cos\left(\Delta\theta_1 - \frac{\Phi_B}{\Phi_0} \pi\right)\right] \]

可以注意到 \( L_{\text{SQUID}} \) 的值會受到外加磁通 \( \Phi_B \) 的影響，這為後來 Tunable Transmon 調整頻率的關鍵。定義變數 \( \Phi \)： \[ \Phi \equiv \frac{\Delta\theta_1}{\pi} \Phi_0 - \Phi_B = \frac{\Phi_0}{\pi} \left(\Delta\theta_1 - \frac{\Phi}{\Phi_0} \pi\right) \] 並有： \[ \dot{\Phi} = \frac{\Phi_0}{\pi} \dot{\Delta\theta_1} \] 電壓 \( V \) 和電流 \( I \) 分別為： \[ V = \frac{1}{2} \dot{\Phi}, \quad I = 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \sin\left(\frac{\Phi}{\Phi_0} \pi\right) \]

固定外場 \( \Phi_B \) 下，一組 SQUID 儲存的能量為： \[ E = \int IV \, dt = \int \left[2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \sin\left(\frac{\Phi}{\Phi_0} \pi\right) \cdot \frac{1}{2} \dot{\Phi}\right] dt \] 化簡得： \[ E = I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \int \sin\left(\frac{\Phi}{\Phi_0} \pi\right) d\Phi \] \[ E = -\frac{I_0 \Phi_0}{\pi} \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \cos\left(\frac{\pi}{\Phi_0} \Phi\right) \]

▲由兩個約瑟夫森節組合成可調電感值的\(LC\)電路。