科普介紹

Ref: DOI:10.48550/arXiv.2203.04164

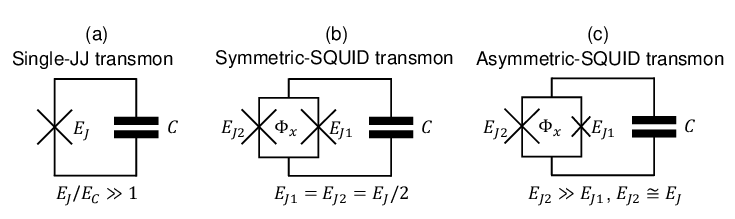
前文提及約瑟夫森節具有電感性質，Transmon即是LC電路中的電感替換成約瑟夫森節。本節直接討論 Tunable Transmon，採用 SQUID 當作電感。實務上因為材料製作的不均一性，不同 Transmon 會有不一樣的特性，如果採用 Tunable Transmon，可以透過微調磁通量 \( \Phi_B \) 的方式使 Qubit 性質一致。此外，我們在前面量子化 LC 電路時，\([ \Phi, Q ] = i\hbar\) 是一對正則變量，利用 SQUID 的推導可以很自然地將磁通量 \( \Phi \) 與相位差 \( \Delta\theta \) 做聯繫，即： \[ \Phi \equiv \frac{\Delta\theta_1}{\pi} \Phi_0 - \Phi_B \]

現在我們寫下 Hamiltonian： \[ \mathcal{H} = \frac{Q^2}{2C} + \frac{\Phi_\#^2}{2L} = \frac{Q^2}{2C} + \frac{(I_0 \pi)}{2\Phi_0} \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \Phi^2 - \frac{I_0}{24} \left(\frac{\pi}{\Phi_0}\right)^3 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \Phi^4 + \cdots \] \[ = \frac{Q^2}{2C} + \frac{\Phi^2}{2L} - \frac{1}{24L} \left(\frac{\pi}{\Phi_0}\right)^2 \Phi^4 + \cdots \] 其中： \[ L = \left(\frac{I_0 \pi}{\Phi_0} \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right)\right)^{-1} \]

現在我們要討論非線性對於能階的改變，前文我們選擇新的變量 \( a \)、\( a^\dagger \)： \[ a = \sqrt{\frac{1}{2\hbar} \sqrt{ \frac{L}{C}}} \left(\sqrt{\frac{C}{L}} \Phi + iQ\right), \quad a^\dagger = \sqrt{\frac{1}{2\hbar} \sqrt{ \frac{L}{C}}} \left(\sqrt{\frac{C}{L}} \Phi - iQ\right) \] 反之： \[ \Phi = \sqrt{\frac{\hbar}{2 }\sqrt{ \frac{L}{C}}} (a^\dagger + a), \quad Q = i\sqrt{\frac{\hbar}{2} \sqrt{ \frac{C}{L}}} (a^\dagger - a) \]

將 Hamiltonian 表達式展開為： \[ \mathcal{H} = \frac{\hbar}{\sqrt{LC}} \left[a^\dagger a + \frac{1}{2}\right] - \frac{1}{24L} \left(\frac{\pi}{\Phi_0}\right)^2 \left[i \sqrt{\frac{\hbar}{2\sqrt{L/C}}} (a^\dagger + a)\right]^4 \] 化簡後： \[ \mathcal{H} = \frac{\hbar}{\sqrt{LC}} \left[a^\dagger a + \frac{1}{2}\right] - \frac{\hbar^2}{96C} \left(\frac{\pi}{\Phi_0}\right)^2 (a^\dagger + a)^4 \] 該表達式包含線性和非線性項，線性項描述的是量子簡諧振子的能階，而非線性項源自於 Josephson 節對於能階的修正。

利用微擾理論，當 \( \mathcal{H} = H_0 + \Delta H \)， \( |E_0^m\rangle \to |E^m\rangle \)、 \( E_0^m \to E^m = E_0^m + \delta E^m \)，我們知道對能階 \( E_0^m \) 的修正 \( \delta E^m \) 為：

\[ \delta E^m = \langle E_0^m | \Delta H | E_0^m \rangle = \langle E_0^m | \left[-\frac{\hbar^2}{96C} \left(\frac{\pi}{\Phi_0}\right)^2 (a^\dagger + a)^4\right] | E_0^m \rangle \]

計算如下：

\[ \langle E_0^m | (a^\dagger + a)^4 | E_0^m \rangle = \langle E_0^m | (aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger)^2 | E_0^m \rangle \]

展開為：

\[ \langle E_0^m | aa(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) + aa^\dagger(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) + a^\dagger a(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) + a^\dagger a^\dagger(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) | E_0^m \rangle \]

因為取期望值，只會留下 \( a, a^\dagger \) 次數相等的項，剩下：

\[ \langle E_0^m | aaa^\dagger a^\dagger + aa^\dagger aa^\dagger + aa^\dagger a^\dagger a + a^\dagger aaa^\dagger + a^\dagger aa^\dagger a + a^\dagger a^\dagger aa | E_0^m \rangle \]

繼續簡化：

\[ \langle E_0^m | a(a^\dagger a + 1)a^\dagger + aa^\dagger aa^\dagger + (a^\dagger a + 1)a^\dagger a + a^\dagger a(a^\dagger a + 1) + a^\dagger aa^\dagger a + a^\dagger (aa^\dagger - 1)a | E_0^m \rangle \]

再整理為：

\[ \langle E_0^m | aa^\dagger aa^\dagger + aa^\dagger + aa^\dagger aa^\dagger + a^\dagger aa^\dagger a + a^\dagger a + a^\dagger aa^\dagger a + a^\dagger a + a^\dagger aa^\dagger a + a^\dagger aa^\dagger a - a^\dagger a | E_0^m \rangle \]

進一步簡化：

\[ \langle E_0^m | 2aa^\dagger aa^\dagger + aa^\dagger + 4a^\dagger aa^\dagger a + a^\dagger a | E_0^m \rangle \] \[ = \langle E_0^m | 2(a^\dagger a + 1)(a^\dagger a + 1) + (a^\dagger a + 1) + 4a^\dagger aa^\dagger a + a^\dagger a | E_0^m \rangle \]

最終得到：

\[ \langle E_0^m | 6a^\dagger aa^\dagger a + 6a^\dagger a + 3 | E_0^m \rangle = 6m^2 + 6m + 3 \]

定義能階差：

\[ \Delta E^m_{m-1} = \frac{\hbar}{\sqrt{LC}} - \frac{\hbar^2}{96C} \left(\frac{\pi}{\Phi_0}\right)^2 \left\{6[m^2 - (m-1)^2] + 6\right\} \]

\[ = \frac{\hbar}{\sqrt{LC}} - \frac{\hbar^2 \pi^2}{96C} \frac{e^2}{\pi^2 \hbar^2} \left[6(2m - 1) + 6\right] \]

最終得到：

\[ \Delta E^m_{m-1} = \frac{\hbar}{\sqrt{LC}} - m\frac{e^2}{8C} \]

計算 \( \Delta E^{21} - \Delta E^{10} \)：

\[ \Delta E^{21} - \Delta E^{10} = \left(\frac{\hbar}{\sqrt{LC}} - 2\frac{e^2}{8C}\right) - \left(\frac{\hbar}{\sqrt{LC}} - \frac{e^2}{8C}\right) \]

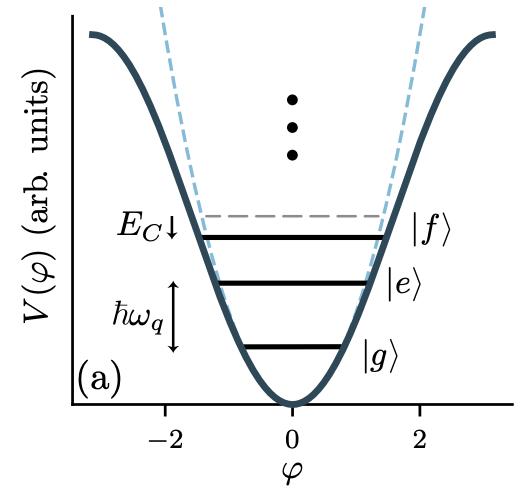
\[ = -\frac{e^2}{8C} \equiv -E_C \]

\( E_C \) 表示其非線性效應。

Ref: DOI:10.1103/RevModPhys.93.025005