科普介紹

量子物理中常見的簡諧振蕩，經過量子化後能產生離散的能階，這正是量子計算基礎中的量子位元所依賴的概念。量子位元需要以具有量子效應的元件為基礎，利用超導體作為量子材料，結合 LC 振蕩電路的概念，製造出超導量子位元。本節將首先討論 LC 電路的量子化過程。

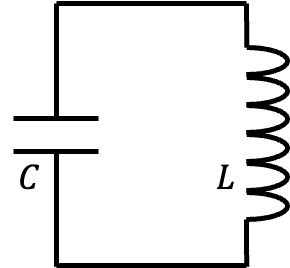
▲一個基礎的 \(LC\) 振蕩電路包含一個電感 \(L\) 和一個電容 \(C\)。定義電容攜帶的電荷為 \(Q\)，當電容儲存的電荷改變速度（即 \(\dot{Q}\)）時，即表示電路上的流動電流。電容和電感分別儲存的能量可表達為： \[ E_C = \frac{Q^2}{2C}, \quad E_L = \frac{L\dot{Q}^2}{2}. \] 我們可以將 \(E_L\) 視為動能項 \(T\)，將 \(E_C\) 視為位能項 \(U\)，從而定義拉格朗日量 \(L\)： \[ \mathcal{L}(\dot{Q}, Q) = T - U = \frac{L\dot{Q}^2}{2} - \frac{Q^2}{2C}. \]

根據歐拉-拉格朗日方程： \[ \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{Q}} - \frac{\partial \mathcal{L}}{\partial Q} = 0, \] 我們得到： \[ L\ddot{Q} + \frac{Q}{C} = 0 \implies \ddot{Q} + \frac{Q}{LC} = 0, \] 即描述一個以頻率 \(\omega = \frac{1}{\sqrt{LC}}\) 振蕩的簡諧運動。