Qubit Physics

In quantum physics, a harmonic oscillator, after quantization, produces discrete energy levels, which form the foundational concept of qubits in quantum computing. Qubits rely on components exhibiting quantum effects. By using superconductors as quantum materials combined with the concept of LC oscillatory circuits, superconducting qubits can be manufactured. This section will first discuss the quantization process of LC circuits.

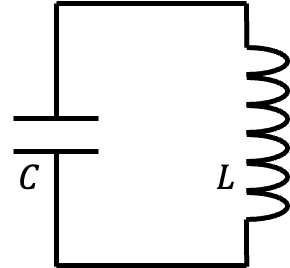
A basic \(LC\) oscillatory circuit consists of an inductor \(L\) and a capacitor \(C\). Defining the charge stored in the capacitor as \(Q\), the rate of change of \(Q\) (\(\dot{Q}\)) represents the current in the circuit. The energy stored in the capacitor and inductor can be expressed as: \[ E_C = \frac{Q^2}{2C}, \quad E_L = \frac{L\dot{Q}^2}{2}. \] We can interpret \(E_L\) as the kinetic energy term \(T\) and \(E_C\) as the potential energy term \(U\), thereby defining the Lagrangian \(\mathcal{L}\): \[ \mathcal{L}(\dot{Q}, Q) = T - U = \frac{L\dot{Q}^2}{2} - \frac{Q^2}{2C}. \]

According to the Euler-\mathcal{L}agrange equation: \[ \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{Q}} - \frac{\partial \mathcal{L}}{\partial Q} = 0, \] we obtain: \[ L\ddot{Q} + \frac{Q}{C} = 0 \implies \ddot{Q} + \frac{Q}{LC} = 0, \] which describes simple harmonic motion with a frequency of \(\omega = \frac{1}{\sqrt{LC}}\).

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.