Qubit Physics

The wavefunction \(\Psi\) of a particle with charge \(q\) satisfies the Schrödinger equation: \[ i\hbar \partial_t \Psi = \frac{\hat{p}^2}{2m} \Psi + V\Psi, \] where the momentum operator \(\hat{p}\) under the influence of an electromagnetic potential \((\phi, \mathbf{A})\) is expressed as (in SI units): \[ \hat{p} = \frac{\hbar}{i} \nabla - q\mathbf{A}. \] Substituting into the Schrödinger equation gives: \[ i\hbar \partial_t \Psi = \frac{1}{2m} \left( \frac{\hbar}{i} \nabla - q\mathbf{A} \right) \left( \frac{\hbar}{i} \nabla \Psi - q\mathbf{A}\Psi \right) + V\Psi. \] Expanding this yields: \[ i\hbar \partial_t \Psi = -\frac{\hbar^2}{2m} \nabla^2 \Psi - \frac{q}{2m} \frac{\hbar}{i} \nabla \cdot (\mathbf{A}\Psi) - \frac{q}{2m} \frac{\hbar}{i} \mathbf{A} \cdot \nabla \Psi + \frac{q^2 A^2}{2m} \Psi + V\Psi. \]

Its conjugate equation is: \[ -i\hbar \partial_t \Psi^* = -\frac{\hbar^2}{2m} \nabla^2 \Psi^* + \frac{q}{2m} \frac{\hbar}{i} \nabla \cdot (\mathbf{A} \Psi^*) + \frac{q}{2m} \frac{\hbar}{i} \mathbf{A} \cdot \nabla \Psi^* + \frac{q^2 A^2}{2m} \Psi^* + V\Psi^*. \]

Multiplying the first equation by \(\Psi^*\) and the second equation by \(\Psi\), and subtracting the two, we get: \[ i\hbar (\Psi^* \partial_t \Psi + \Psi \partial_t \Psi^*) = -\frac{\hbar^2}{2m} (\Psi^* \nabla^2 \Psi - \Psi \nabla^2 \Psi^*) - \frac{q}{2m} \frac{\hbar}{i} \left[ \Psi^* \nabla \cdot (\mathbf{A}\Psi) + \Psi \nabla \cdot (\mathbf{A}\Psi^*) + \Psi^* \mathbf{A} \cdot \nabla \Psi + \Psi \mathbf{A} \cdot \nabla \Psi^* \right]. \] Simplifying: \[ i\hbar \partial_t (\Psi^* \Psi) = -\frac{\hbar^2}{2m} \nabla \cdot (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q}{2m} \frac{\hbar}{i} \nabla \cdot (2\mathbf{A} \Psi^* \Psi). \]

Dividing by \(i\hbar\), we get: \[ \partial_t (\Psi^* \Psi) = -\nabla \cdot \left[ \frac{\hbar}{2mi} (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q\mathbf{A}}{m} \Psi^* \Psi \right]. \] Comparing this with the continuity equation: \[ \partial_t \rho + \nabla \cdot \mathbf{J} = 0, \] where \(\rho = \Psi^* \Psi\) is the probability density, we identify the probability current as: \[ \mathbf{J} = \frac{\hbar}{2mi} (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q\mathbf{A}}{m} \Psi^* \Psi. \]

For charged particles, the current density \(\mathbf{J}_q\) is: \[ \mathbf{J}_q = q \mathbf{J} = q \left[ \frac{\hbar}{2mi} (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q\mathbf{A}}{m} \Psi^* \Psi \right]. \] If the wavefunction is expressed in terms of the particle density \(n(\mathbf{r})\) and phase \(\theta(\mathbf{r})\) as \(\Psi \sim \sqrt{n(\mathbf{r})} e^{i\theta(\mathbf{r})}\), then: \[ \mathbf{J}_q = q\frac{\hbar}{m} n(\mathbf{r}) \left[ \nabla \theta(\mathbf{r}) - \frac{q\mathbf{A}}{\hbar} \right]. \]

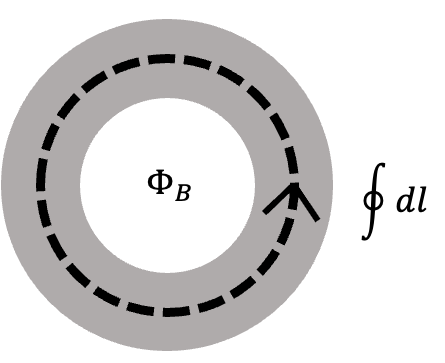
Under topological conditions, and using Stokes' theorem: \[ \int \nabla \times \left[ \nabla \theta(\mathbf{r}) - \frac{q\mathbf{A}}{\hbar} \right] \cdot d\mathbf{S} = \int \nabla \times (\nabla \theta(\mathbf{r})) \cdot d\mathbf{S} - \frac{q}{\hbar} \int (\nabla \times \mathbf{A}) \cdot d\mathbf{S}, \] simplifying to: \[ \oint \nabla \theta(\mathbf{r}) \cdot d\mathbf{l} - \frac{q}{\hbar} \Phi_B = \begin{cases} 0, & \text{if the loop is without a hole}, \\ 2\pi N, & \text{if the loop encloses a hole}. \end{cases} \]

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.