Qubit Physics

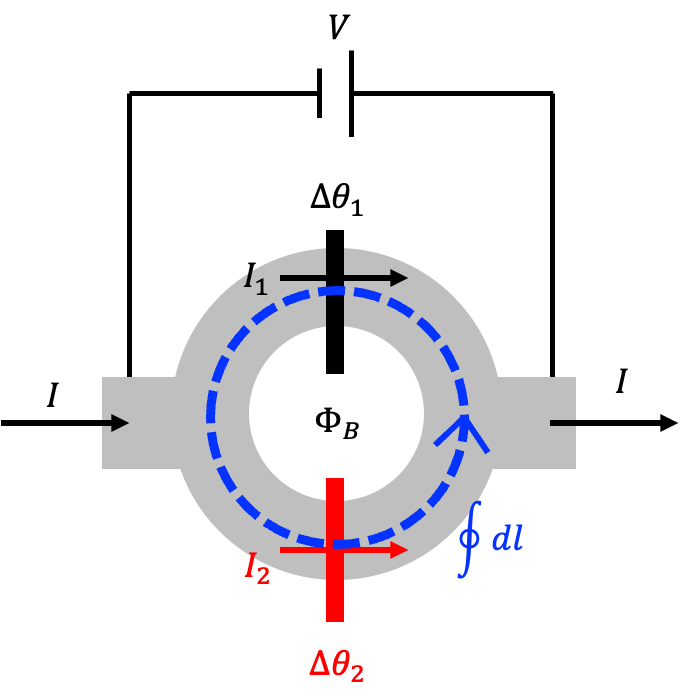
Two Josephson junctions, \(J_1\) and \(J_2\), are connected to form a closed loop, with a magnetic flux \(\Phi_B\) and voltage \(V\) applied. According to the previous section, the integral of the superconducting wavefunction phase around the loop must satisfy: \[ \oint \nabla \theta(r) \cdot d\vec{l} - \frac{q}{\hbar} \Phi_B = 2\pi N. \] Since discontinuities at the junctions contribute \(\Delta\theta_1\) and \(\Delta\theta_2\), and with \(q = -2e\), this becomes: \[ \Delta\theta_2 - \Delta\theta_1 + 2\pi \frac{\Phi_B}{\Phi_0} = 2\pi N, \] leading to: \[ \Delta\theta_2 = \Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0} + 2\pi N. \]

When the entire SQUID loop carries a current \(I = I_1 + I_2\), and using the Josephson current relation from the previous section (assuming a symmetric SQUID with both junctions having the same \(I_c\)), we compute: \[ I = I_1 + I_2 = I_0 (\sin\Delta\theta_1 + \sin\Delta\theta_2). \] Substituting \(\Delta\theta_2\): \[ I = I_0 \left[\sin\Delta\theta_1 + \sin\left(\Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0} + 2\pi N\right)\right]. \] Simplifying (noting that \(N\) is an integer and does not affect the sine function): \[ I = I_0 \left[\sin\Delta\theta_1 + \sin\left(\Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0}\right)\right]. \] Using trigonometric identities: \[ I = I_0 \left[2 \sin\left(\frac{\Delta\theta_1 + \Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0}}{2}\right) \cos\left(\frac{\Delta\theta_1 - \Delta\theta_1 + 2\pi \frac{\Phi_B}{\Phi_0}}{2}\right)\right]. \] This simplifies to: \[ I = 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \sin\left(\Delta\theta_1 - \frac{\Phi_B}{\Phi_0} \pi\right). \]

From the previous section, Josephson junctions exhibit inductive properties. Similarly, we can discuss the inductance of the SQUID. Differentiating the current with respect to time gives: \[ \dot{I} = 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \cos\left(\Delta\theta_1 - \frac{\Phi_B}{\Phi_0} \pi\right) \dot{\Delta\theta_1}. \] The relationship between \(\dot{\Delta\theta_1}\) and the voltage \(V\) is: \[ V = \frac{\hbar}{2e} \dot{\Delta\theta_1} = \frac{\Phi_0}{2\pi} \dot{\Delta\theta_1}. \] Substituting this, we find the inductance: \[ L_{\text{SQUID}}(\Delta\theta_1, \Phi_B) = \left[\frac{2\pi}{\Phi_0} \cdot 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \cos\left(\Delta\theta_1 - \frac{\Phi_B}{\Phi_0} \pi\right)\right]. \]

Notice that the value of \(L_{\text{SQUID}}\) is influenced by the external magnetic flux \(\Phi_B\), which is key for tuning the frequency in Tunable Transmons. Defining the variable \(\Phi\): \[ \Phi \equiv \frac{\Delta\theta_1}{\pi} \Phi_0 - \Phi_B = \frac{\Phi_0}{\pi} \left(\Delta\theta_1 - \frac{\Phi_B}{\Phi_0} \pi\right), \] with: \[ \dot{\Phi} = \frac{\Phi_0}{\pi} \dot{\Delta\theta_1}. \] The voltage \(V\) and current \(I\) are: \[ V = \frac{1}{2} \dot{\Phi}, \quad I = 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \sin\left(\frac{\Phi}{\Phi_0} \pi\right). \]

For a fixed external flux \(\Phi_B\), the energy stored in a SQUID is: \[ E = \int IV \, dt = \int \left[2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \sin\left(\frac{\Phi}{\Phi_0} \pi\right) \cdot \frac{1}{2} \dot{\Phi}\right] dt. \] Simplifying gives: \[ E = I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \int \sin\left(\frac{\Phi}{\Phi_0} \pi\right) d\Phi. \] Resulting in: \[ E = -\frac{I_0 \Phi_0}{\pi} \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \cos\left(\frac{\pi}{\Phi_0} \Phi\right). \]

▲An \(LC\) circuit with tunable inductance formed by two Josephson junctions.

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.