科普介紹

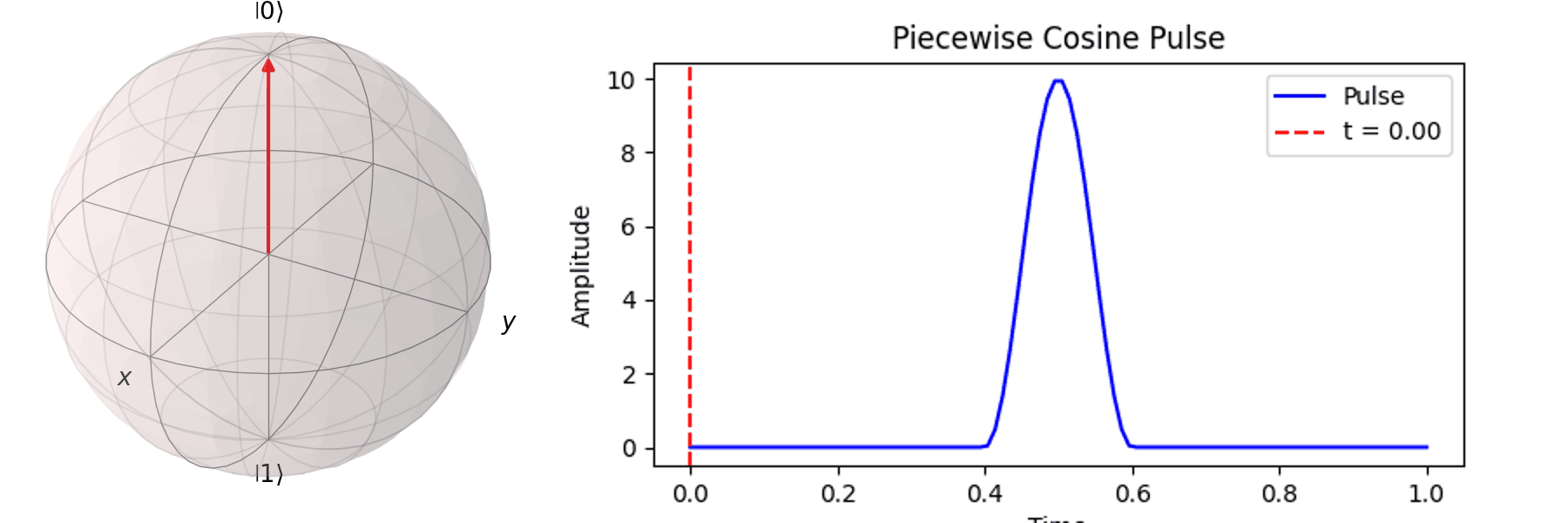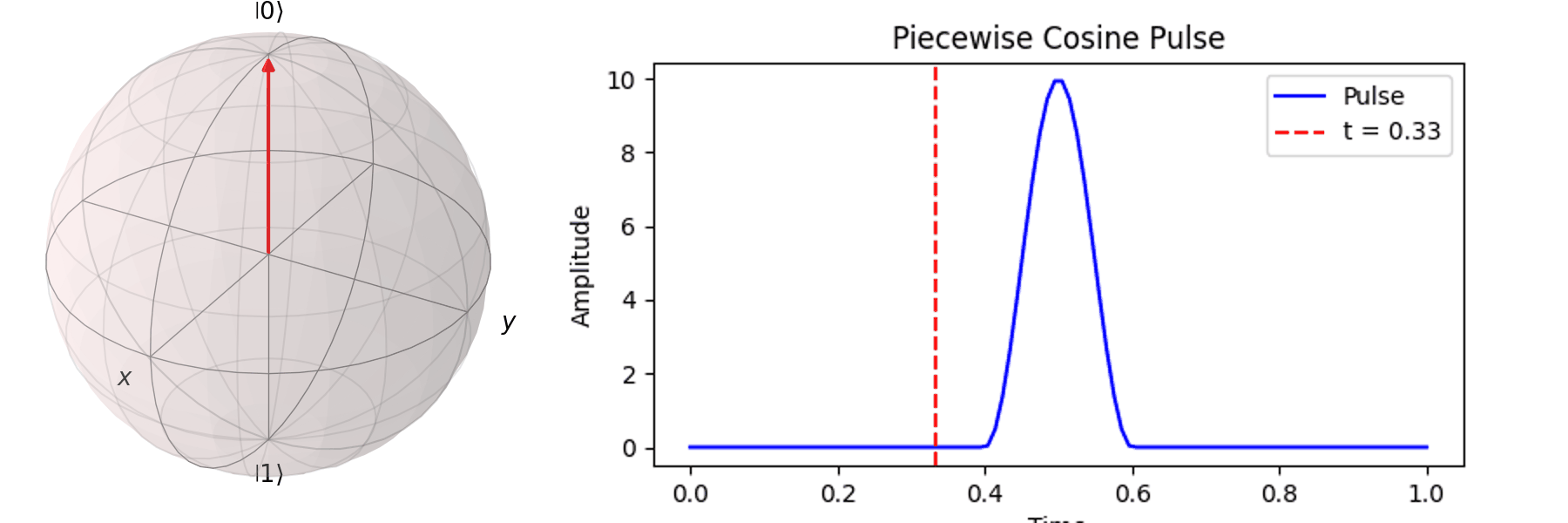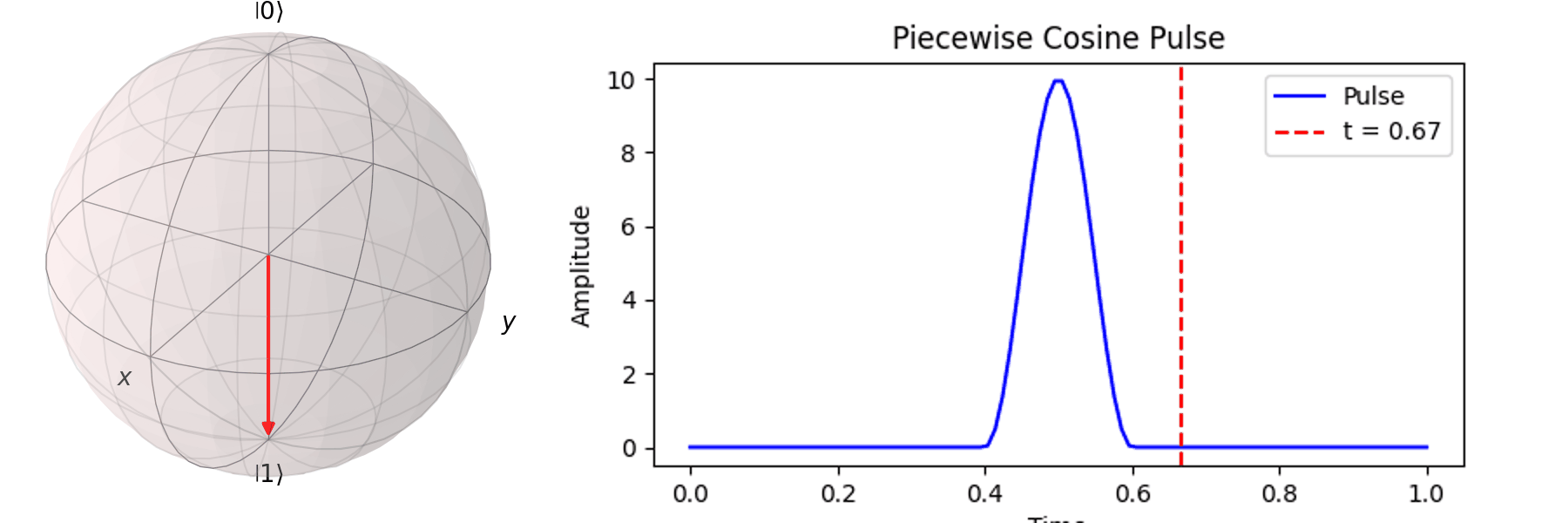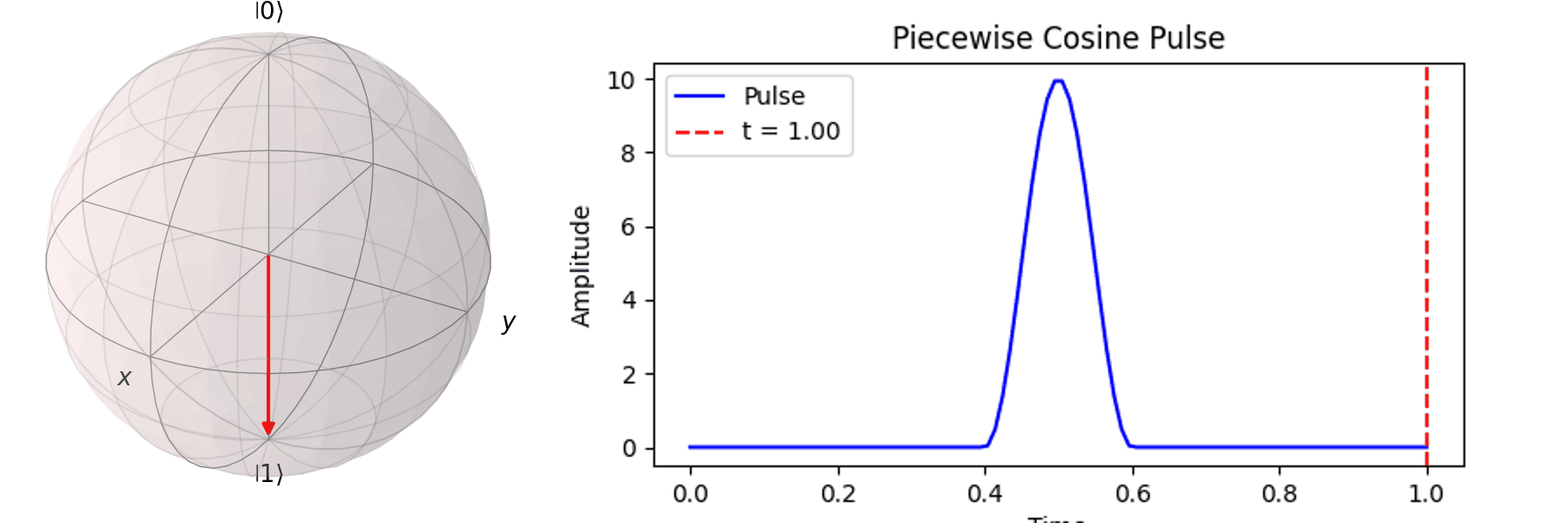
最常見的作法為拉比震盪（Rabi Oscillation），透過施加特定頻率的電場震盪脈衝（Pulse） \( P(t) \)。先來看 Qubit 受到 \( \pi \) -pulse從 \( |\ 0\rangle \rightarrow |\ 1\rangle \)，利用 Bloch 球進行可視化：

控制 Qubit 的主要參數

• 脈衝的振幅（Amplitude \( A \)）： 改變 Qubit 的狀態（Block sphere 的轉角）
• 脈衝的時長（Duration \( T \)）： 改變 Qubit 的狀態（Block sphere 的轉角）
• 脈衝的頻率（Frequency \( \omega_d \)）： 決定是否能精確驅動 Qubit
• 脈衝的包絡（Envelop \( F(t, \tau) \)）： 影響漏態（Leakage）

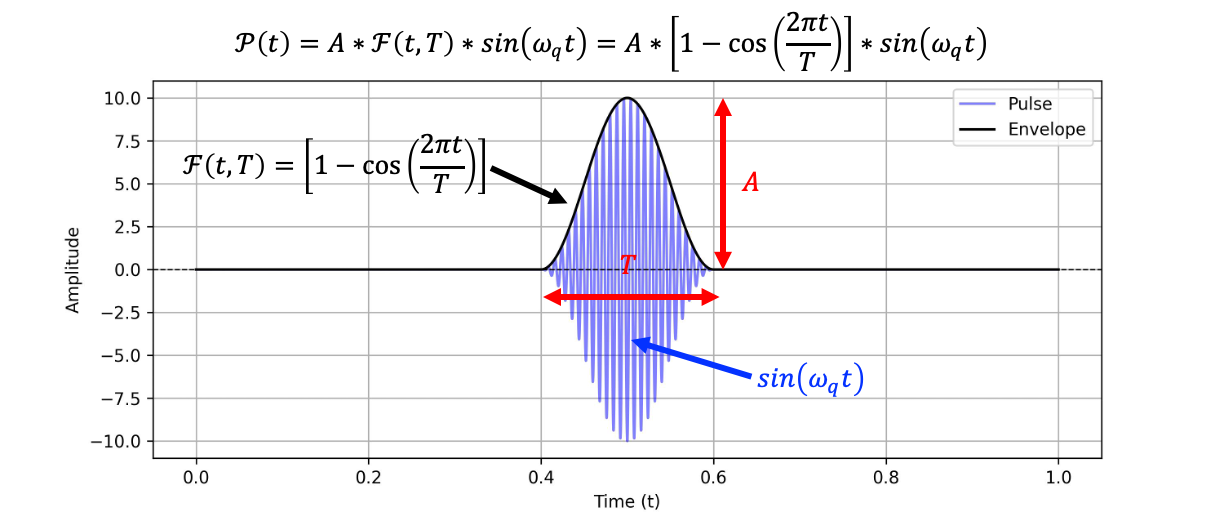
一個完整的脈衝可以表達為： \[ P(t) = A \cdot F(t, \tau) \cdot \sin(\omega_q t) \] 舉例如下：

一般來說因為Qubit相干時間很短，會希望盡可能短的時間操作完Qubit的運算，以超導量子位元而言，相干時間能維持達微秒（μs）當前的技術而言已經很久了，故超導量子位元脈衝多半固定在奈秒等級（\(ns\)）。故操作Qubit的狀態一般採用調控脈衝的振幅的大小來決定轉角。
(實驗中驅動大約\(10ns\)左右\(^a\))
\(^a\) 10.1103/PRXQuantum.5.030353

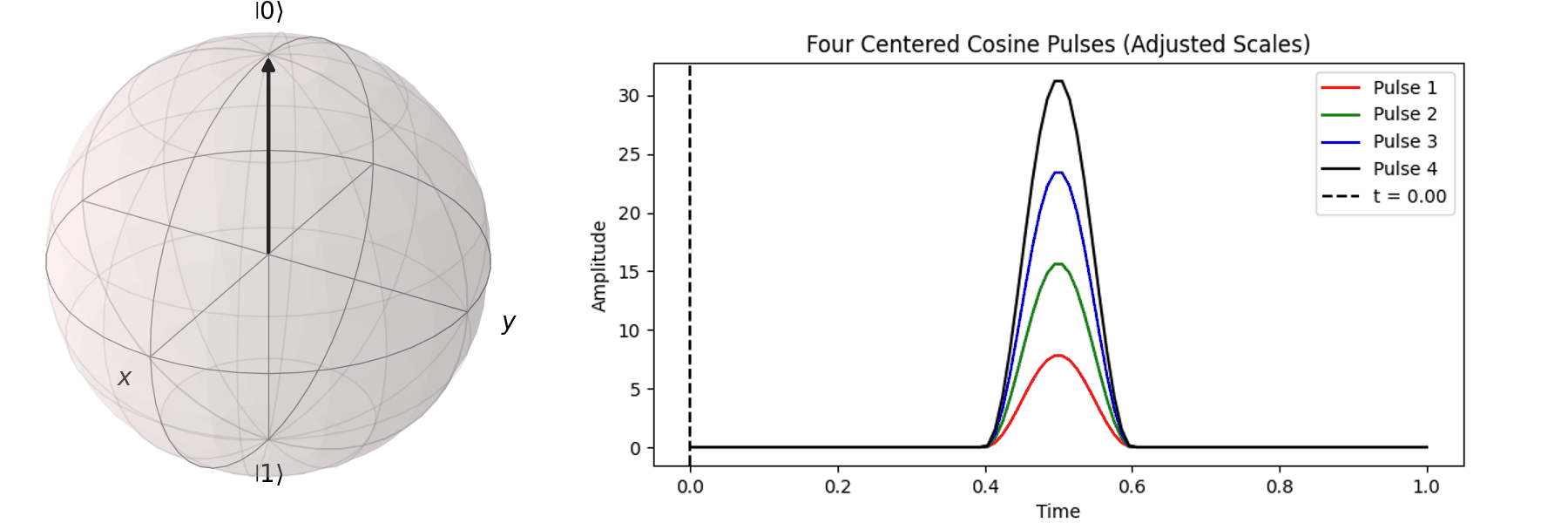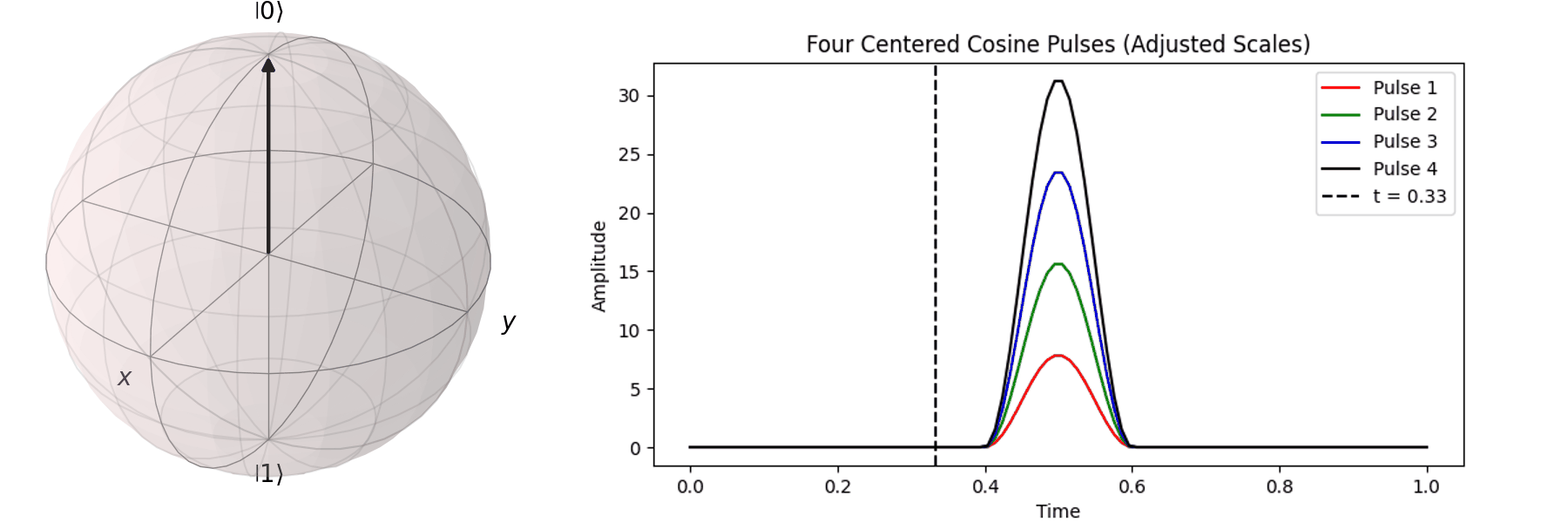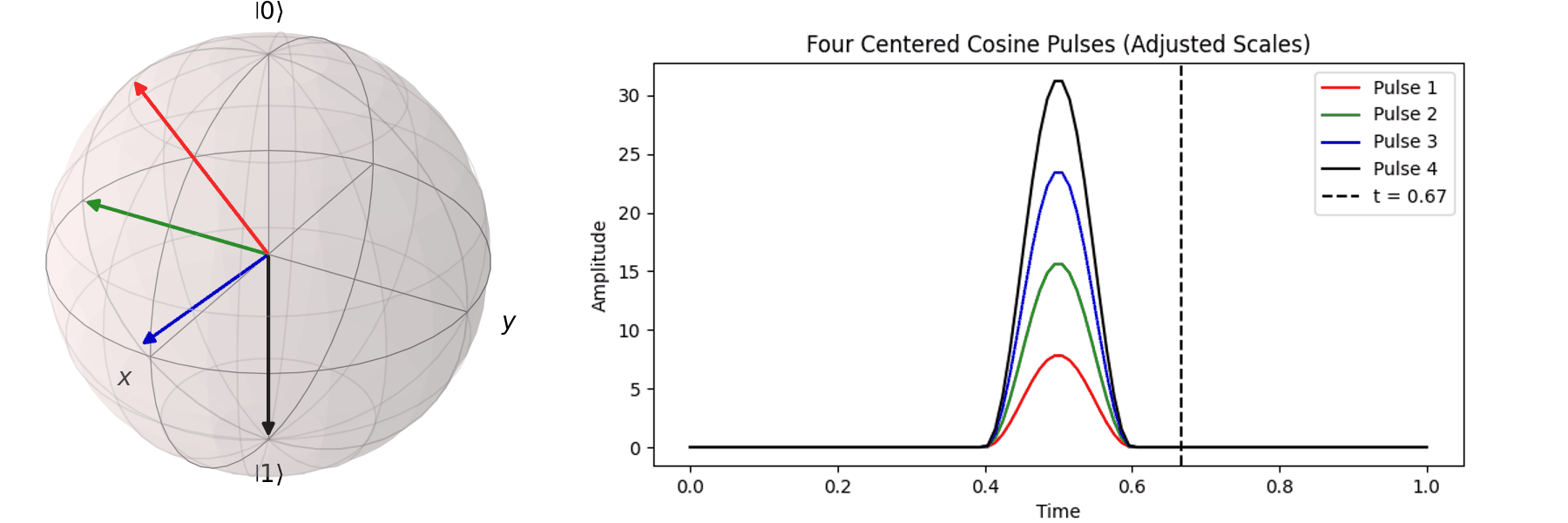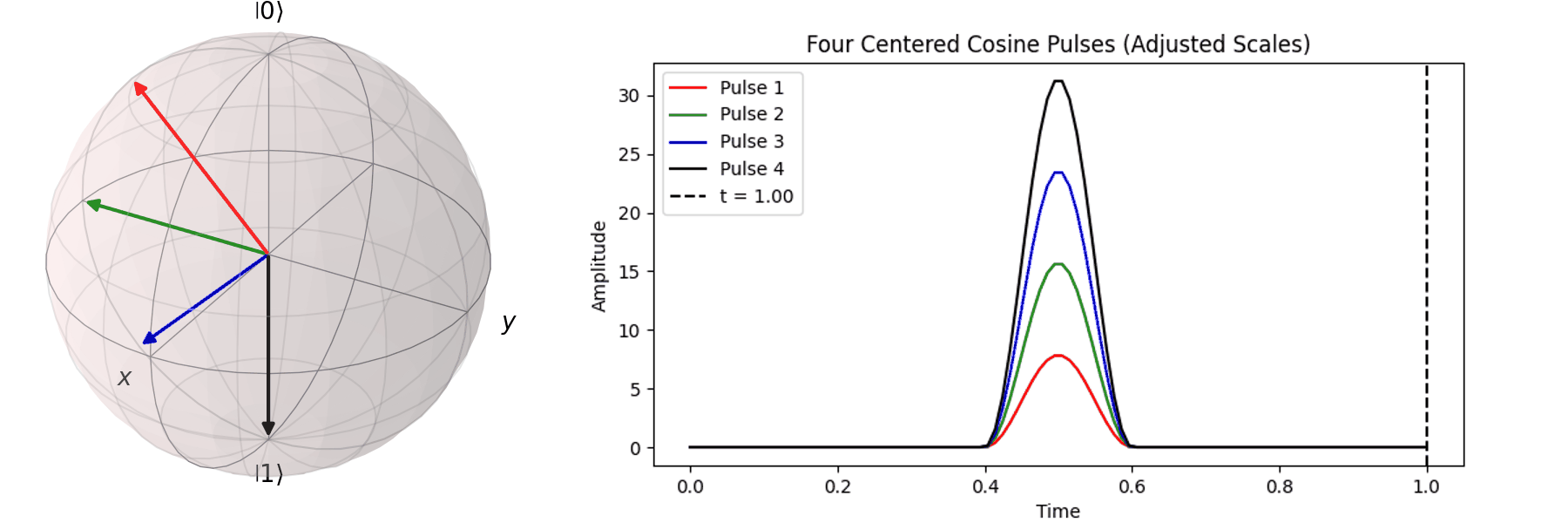
可以藉由 Bloch 球進行可視化，在這邊畫出對\( X \) 軸轉 \(0.25\pi \)、\( 0.5\pi \)、\(0.75\pi\)和\(\pi\)-pulse。可以發現說利用振幅的大小可以決定轉動的角度。

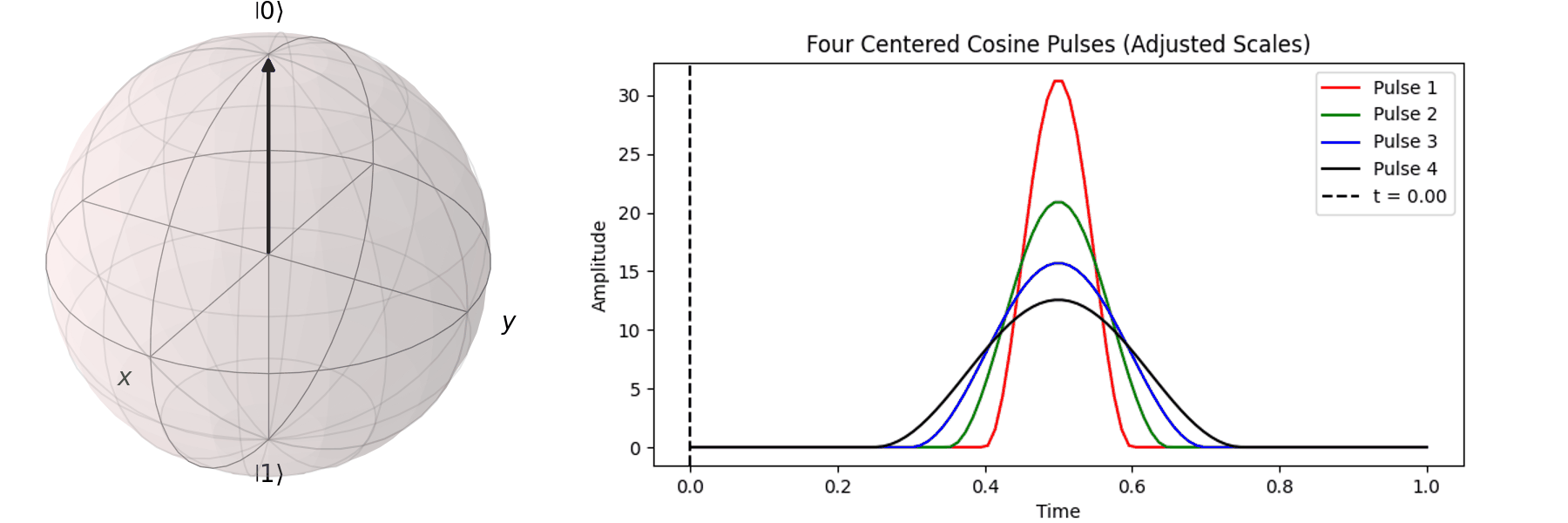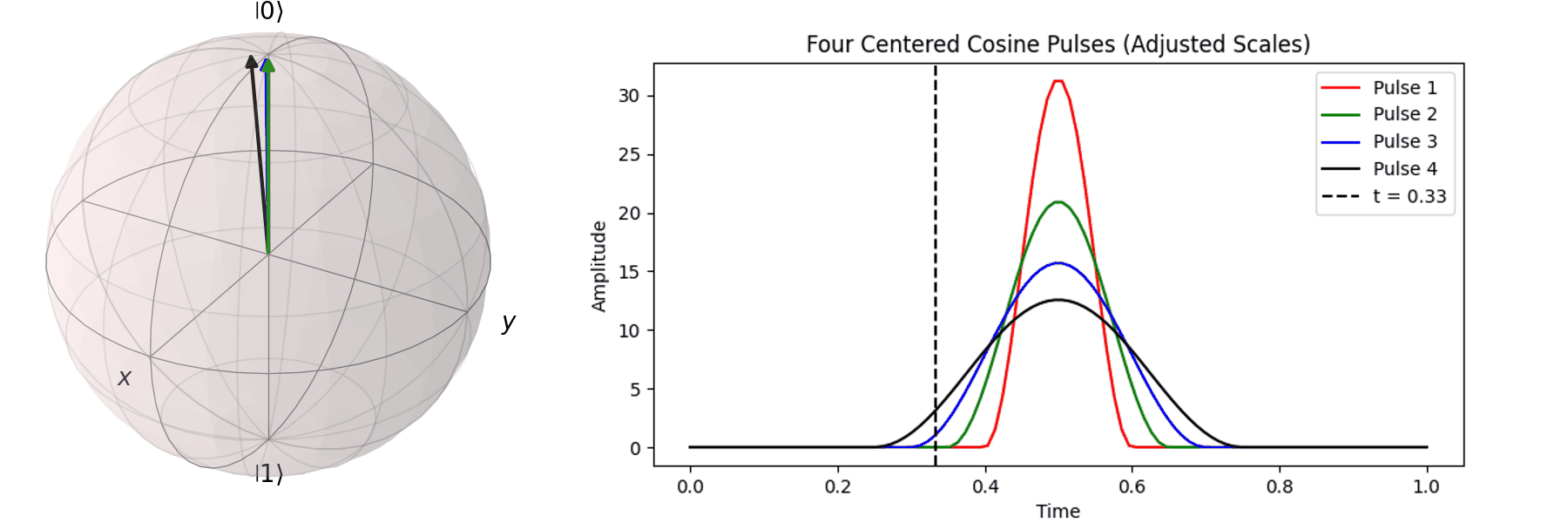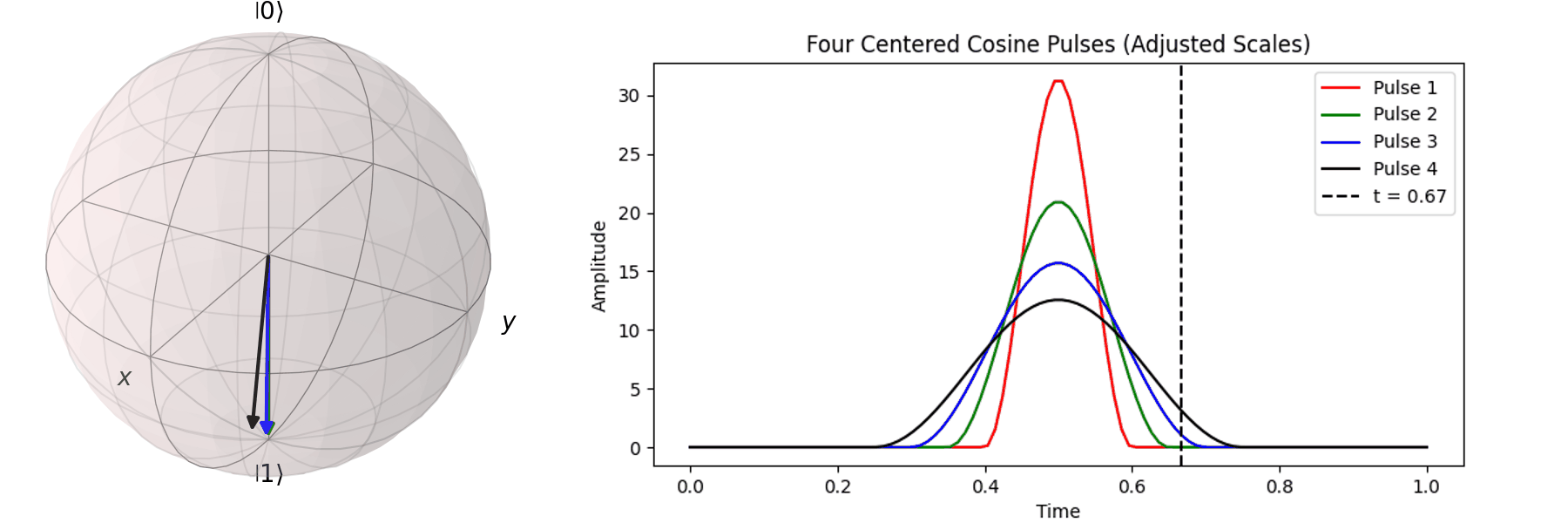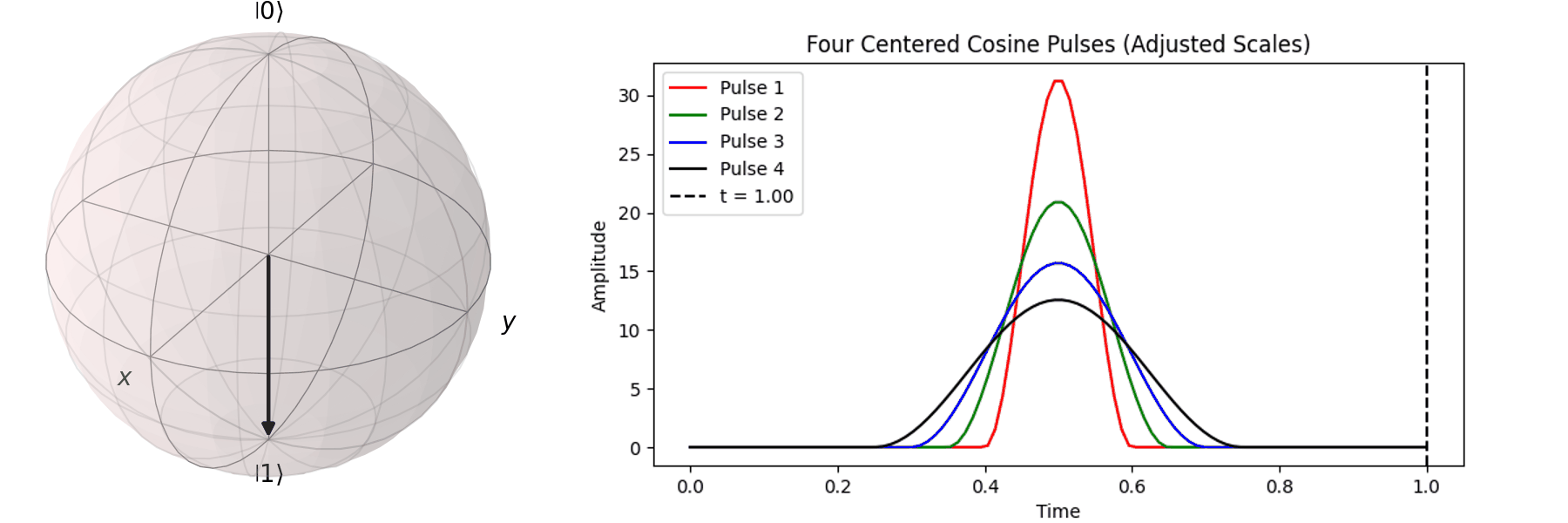
同樣的，也可以討論利用不同脈衝的時長\(T\)來達到相同的 \( \pi \) -pulse從 \( |\ 0\rangle \rightarrow |\ 1\rangle \)

當然，讀者也許會想說，既然超導Qubit相干時間很短，那脈衝的時長\(T\)越短越好。下一節我們就會提到，越尖的脈衝會引入更多不相關的震動頻率，導致Qubit的操作出現誤差。實務上，如何決定脈衝的時長\(T\)與脈衝的震幅\(A\)，一直是Qubit日常校正的一環。良好的校正會得到優質的量子計算效果，反之，光是誤差就可以導致計算不如古典電腦來的準確。

Pulse shape:
10.1103/PRXQuantum.5.030353
10.1103/PhysRevLett.116.020501