超導量子位元是什麼呢?
解析約瑟夫森節如何變成量子位元
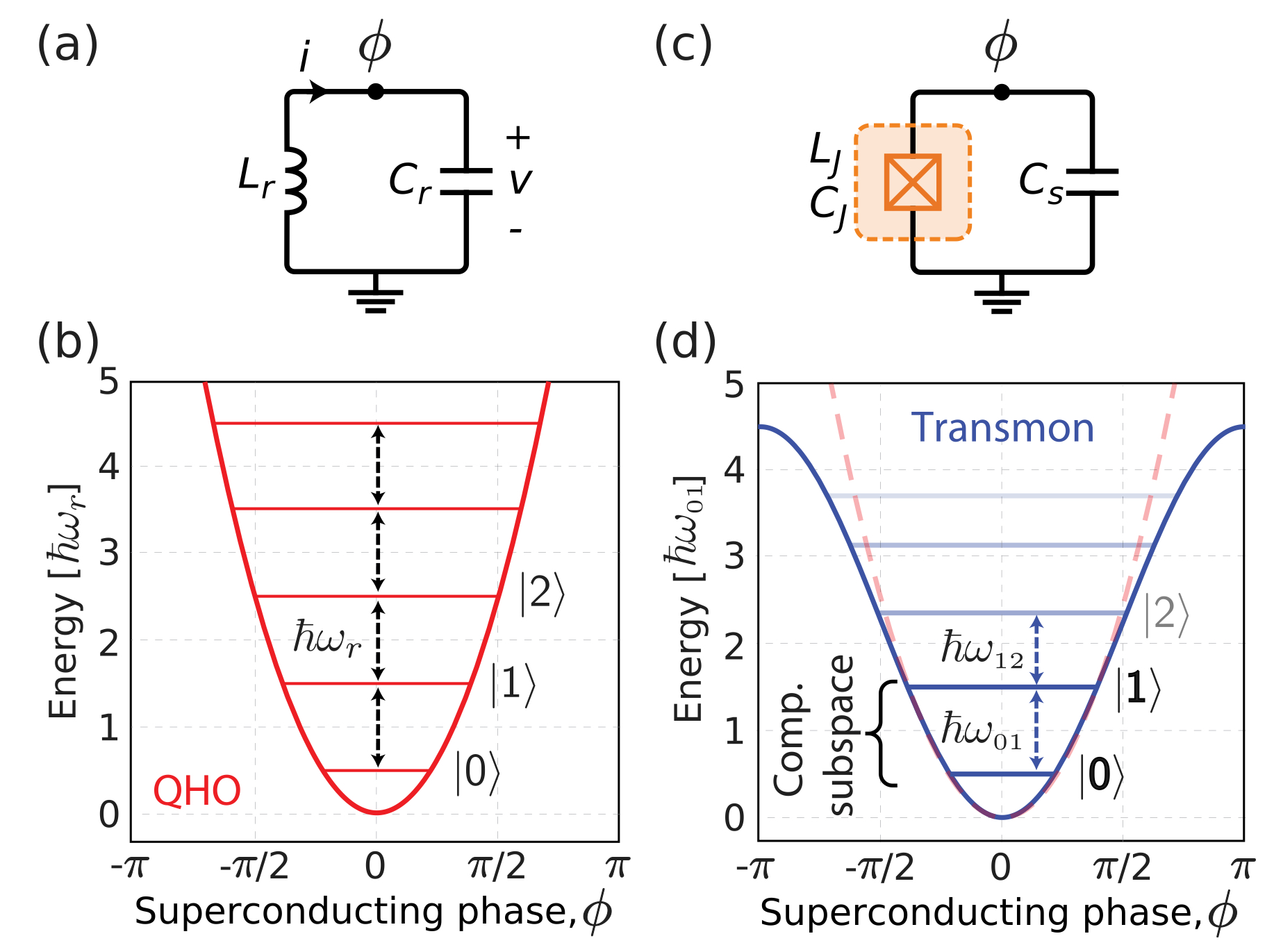
在古典計算中,一系列古典位元以0或1兩個狀態來紀錄資訊,同樣的,量子位元也是利用不同的量子狀態來記錄資訊和計算。最簡單的量子能階概念即為量子簡諧震盪(Quantum Simple Harmonic Oscillator)。想要用電子電路來實踐簡諧震盪,最簡單的方式就是一個\(LC\)電路,由一個電感\(L\)與一個電容\(C\)組成,可以見下圖(a)。古典的簡諧震盪是連續的,但在量子世界裡能階簡諧震盪是不連續的,可以利用不同能階來記錄訊息,我們習慣以\( \ket{0} \)、\(\ket{1}\)、\(\ket{2}\)...或\( \ket{g} \)、\(\ket{e}\)、\(\ket{f}\)...代表不同能量的能階,可以參考下圖(b)。可以看到圖(b)每個能階的差距是相同的,都是\(\hbar \omega_r\)。然而當我們要操作量子位元的時侯,會希望系統被限制在\( \ket{0} \)和\(\ket{1}\)之間作轉換就好,此時就需要非線性元件來區分\( \ket{0} \)和\(\ket{1}\)與其他不想要的能階。約瑟夫森節就是良好的非線性電感元件,如圖(c)。圖(d)可以看到能階差距發生變化,就可以利用能階不同的特性,來操作量子位元。故最基本的超導量子位元即為一個超導電容與一個約瑟夫森節組成!
Ref: 10.1063/1.5089550
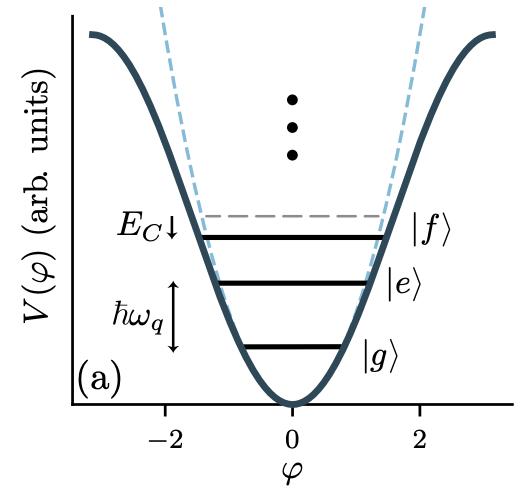
▲此圖也可以很明顯展示超導量子位元能階變化,第二激發態\(\ket{f}\)(或\(\ket{2}\))能量較低。
Ref: 10.1103/RevModPhys.93.025005
 王培儒
王培儒