Qubit Physics

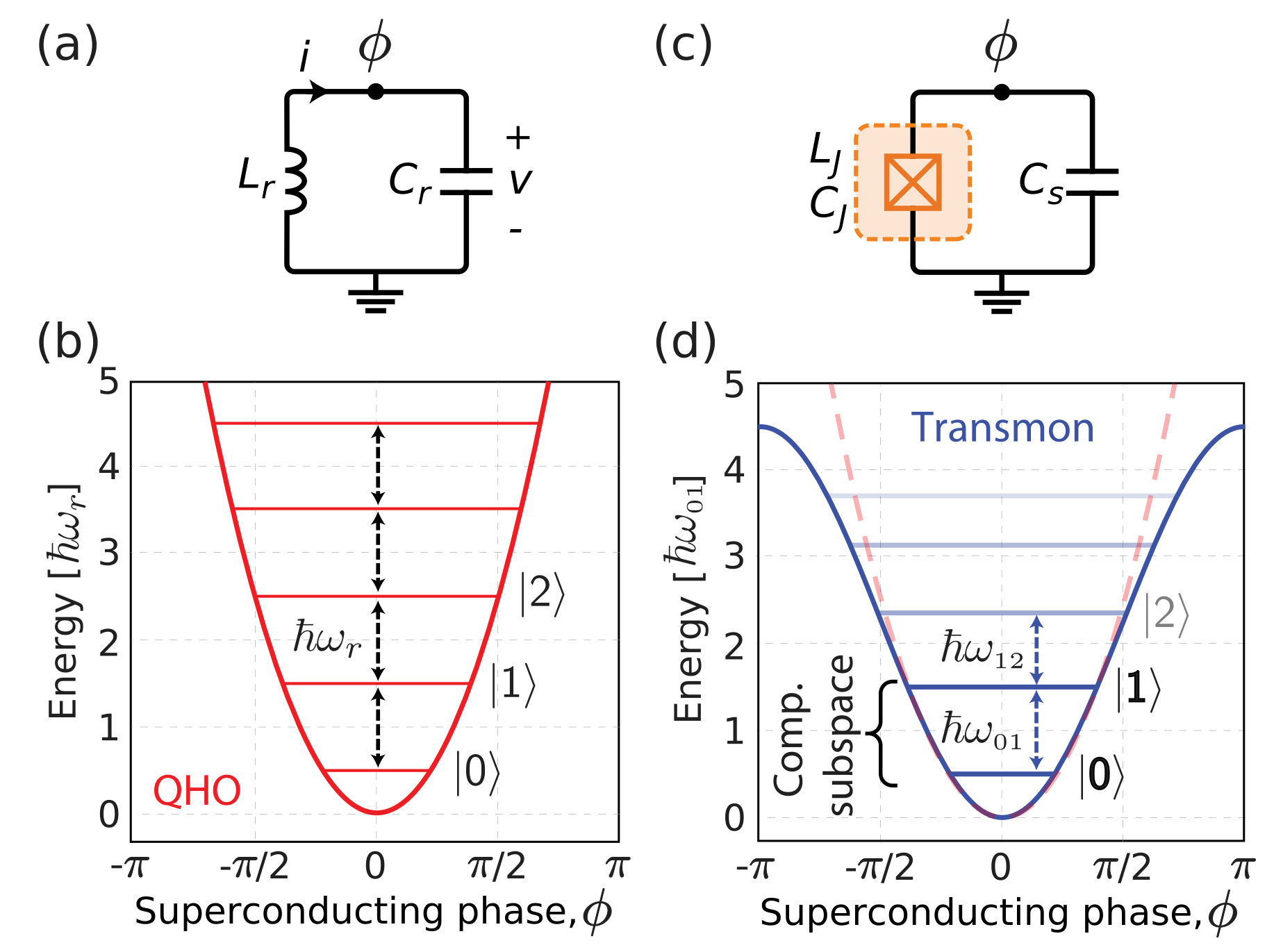
In classical computing, a series of classical bits records information using two states, 0 or 1. Similarly, quantum bits (qubits) record information and perform computations using different quantum states. The simplest concept of quantum energy levels is the Quantum Simple Harmonic Oscillator. To implement a simple harmonic oscillator using an electronic circuit, the simplest approach is an \( LC \) circuit, composed of an inductor \( L \) and a capacitor \( C \), as shown in figure (a). In classical physics, the harmonic oscillator is continuous, but in the quantum world, energy levels are discrete. Different energy levels can be used to encode information, and we typically represent these levels using \( \ket{0} \), \( \ket{1} \), \( \ket{2} \)... or \( \ket{g} \), \( \ket{e} \), \( \ket{f} \)... to denote different energy states, as shown in figure (b). In figure (b), it is evident that the energy gap between each level is the same, \( \hbar \omega_r \). However, when we want to operate a qubit, we prefer the system to be limited to transitions between \( \ket{0} \) and \( \ket{1} \) only. This requires a nonlinear component to distinguish between \( \ket{0} \), \( \ket{1} \), and the unwanted higher energy levels. The Josephson junction is a highly effective nonlinear inductive element, as shown in figure (c). In figure (d), we can see that the energy gaps become unequal, allowing us to utilize this property to operate the qubit. Therefore, the most basic superconducting qubit consists of a superconducting capacitor and a Josephson junction!

Ref: 10.1063/1.5089550

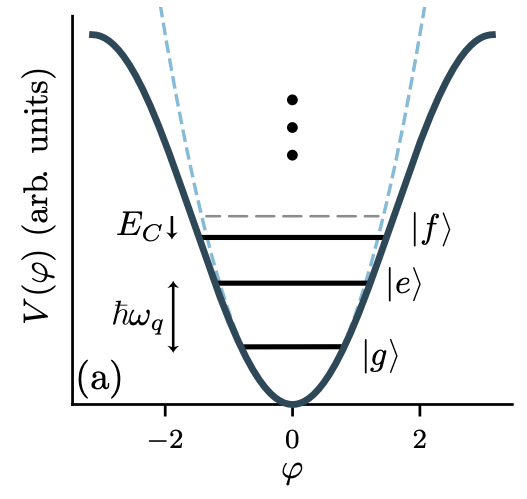
▲ This figure clearly shows the energy level changes in a superconducting qubit. The second excited state \( \ket{f} \) (or \( \ket{2} \)) has lower energy.
Ref: 10.1103/RevModPhys.93.025005

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.