Qubit Physics

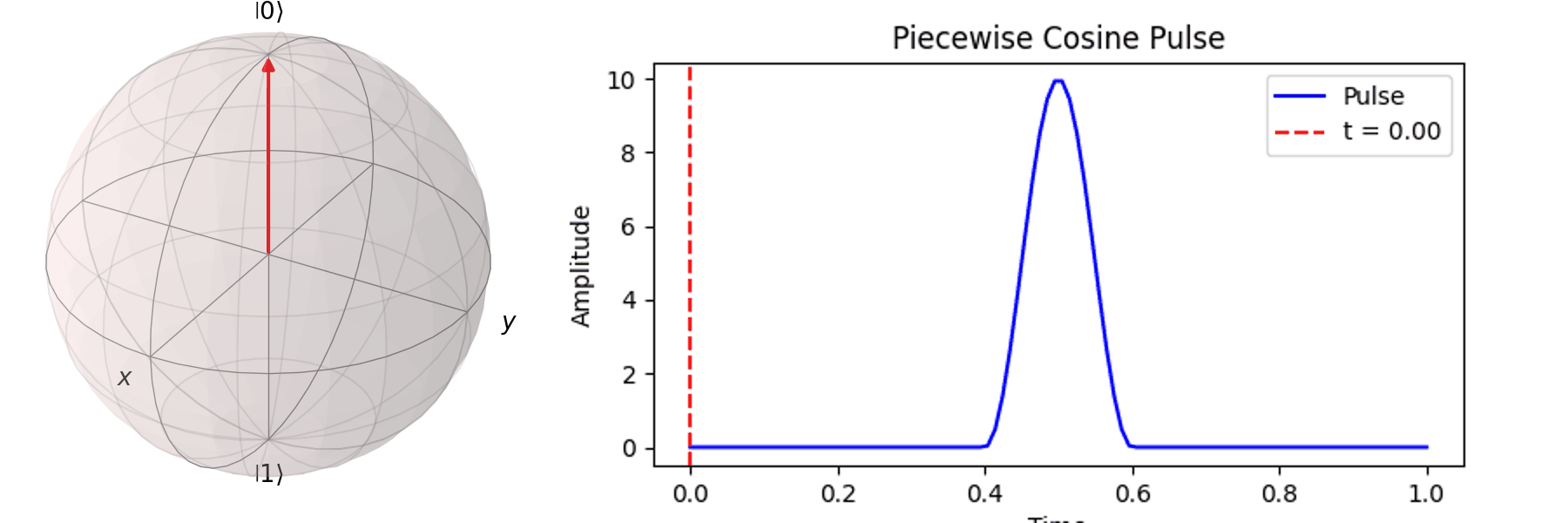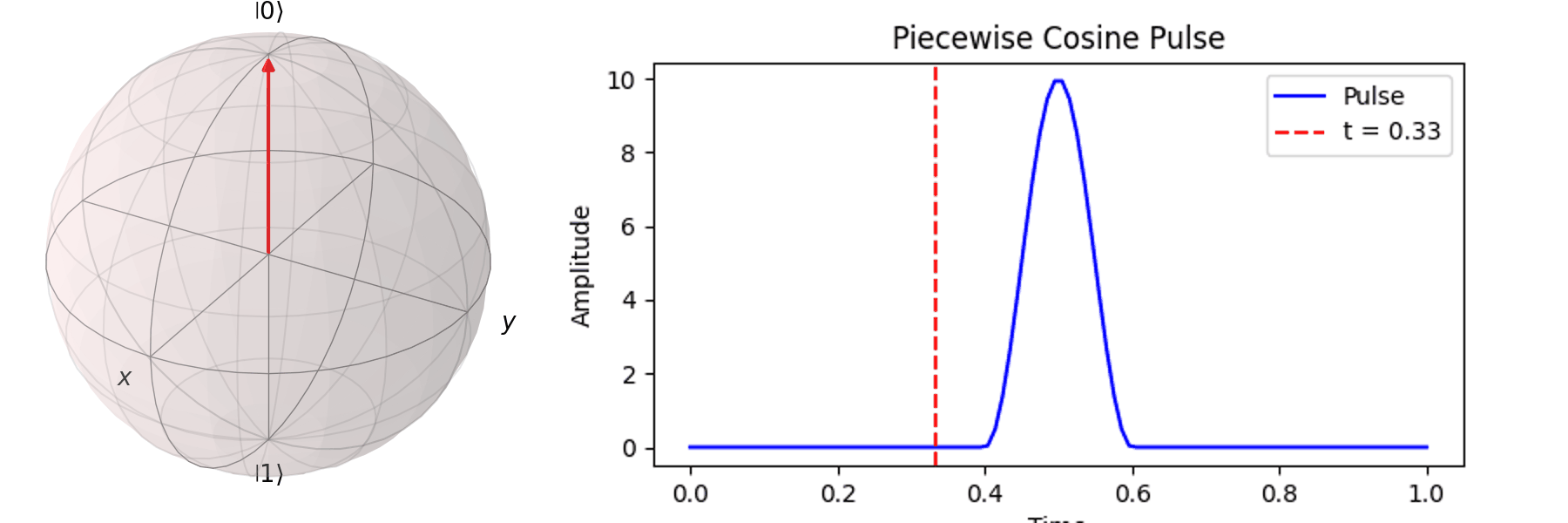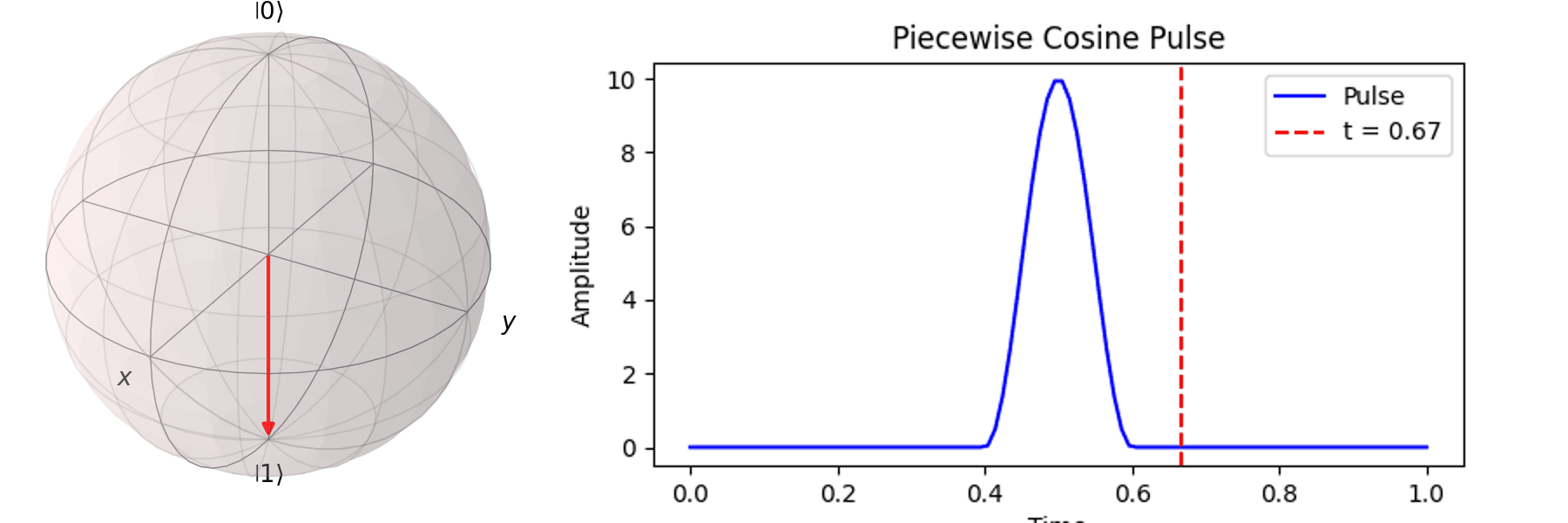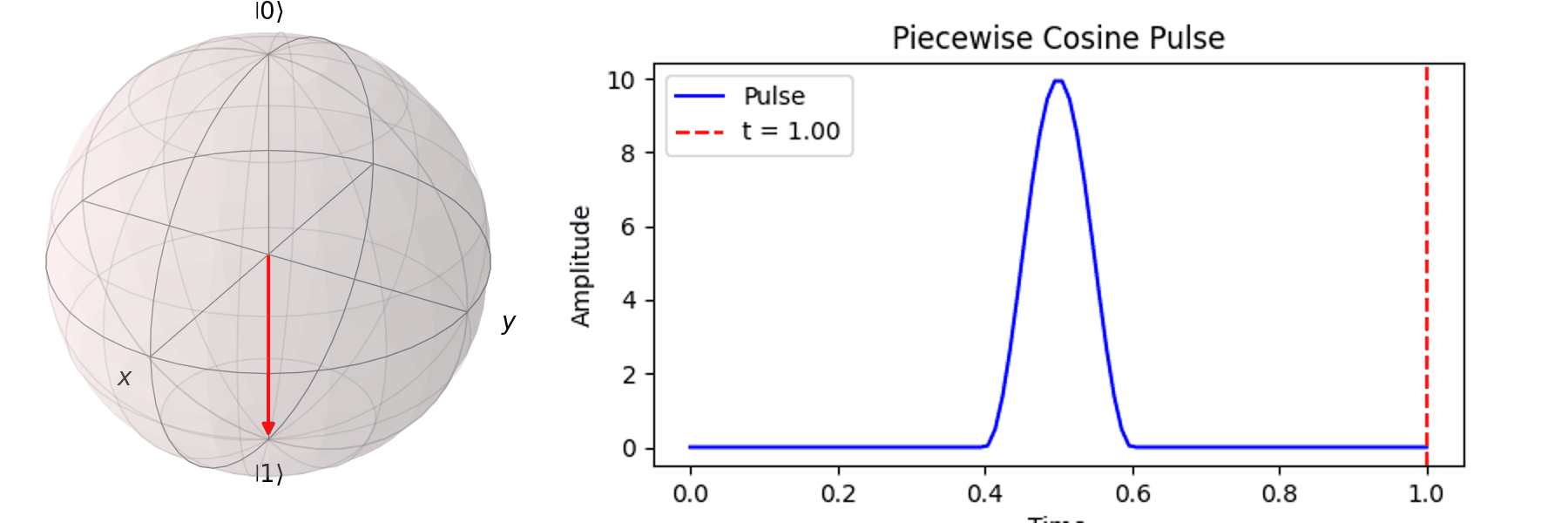
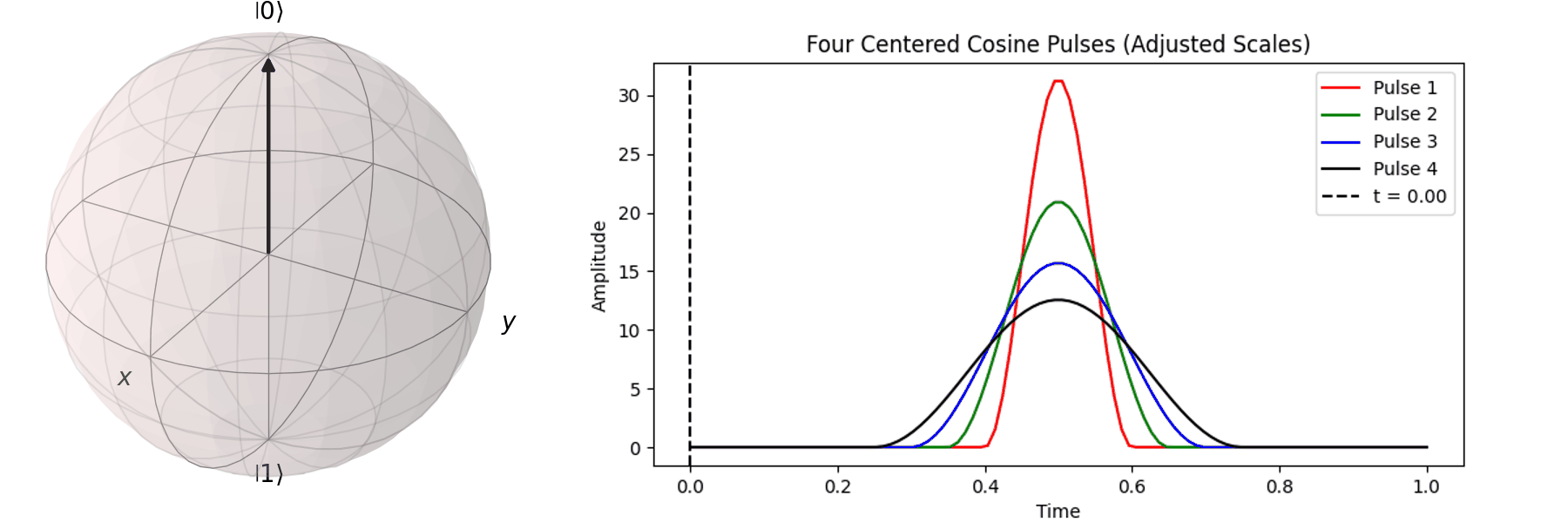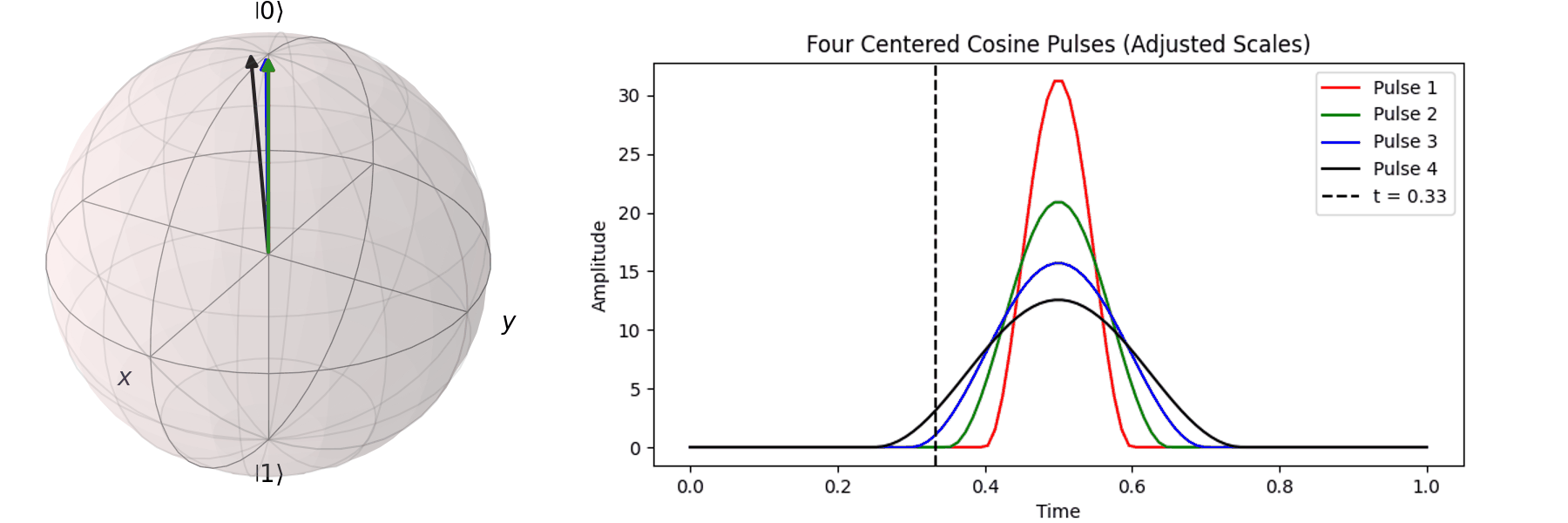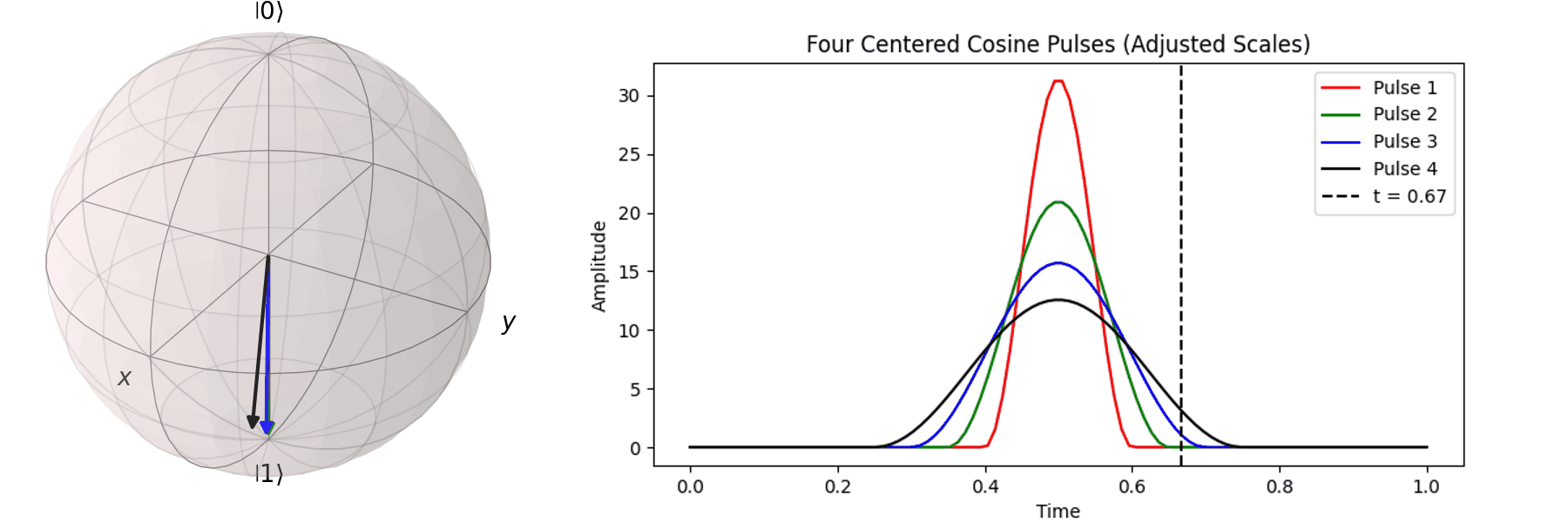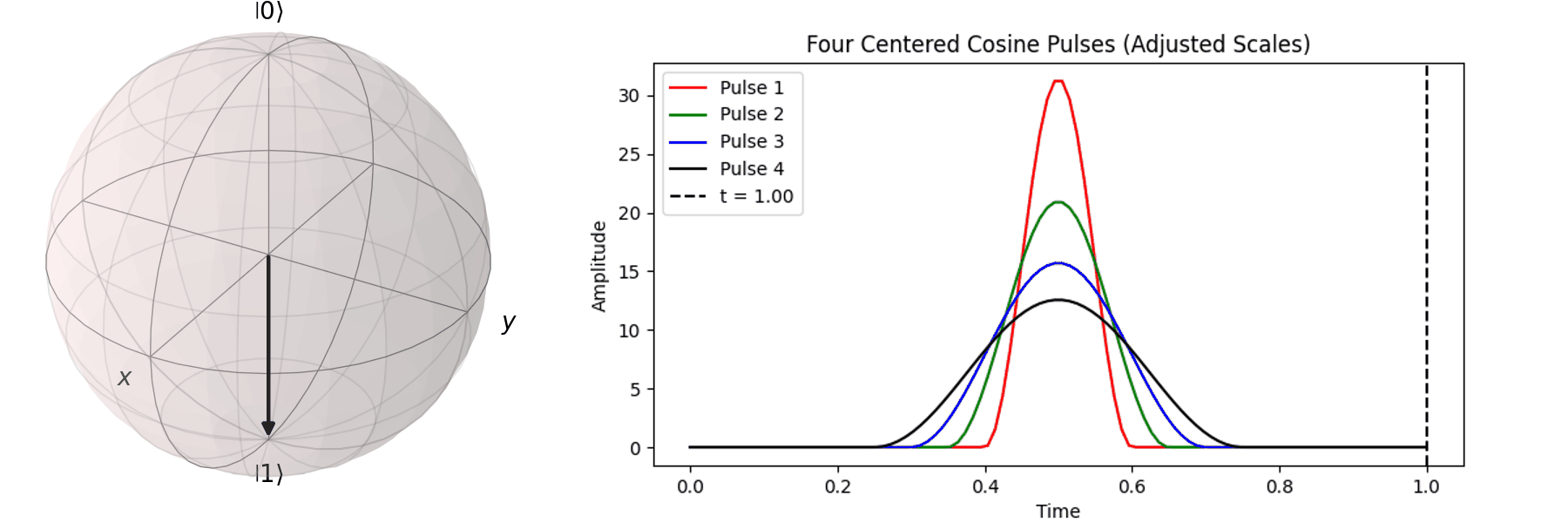
The most common method is Rabi oscillation, achieved by applying an oscillating pulse \( P(t) \) with a specific frequency. Let’s first visualize a Qubit undergoing a \( \pi \)-pulse transition from \( |\ 0\rangle \rightarrow |\ 1\rangle \) using the Bloch sphere:

Main Parameters for Controlling a Qubit

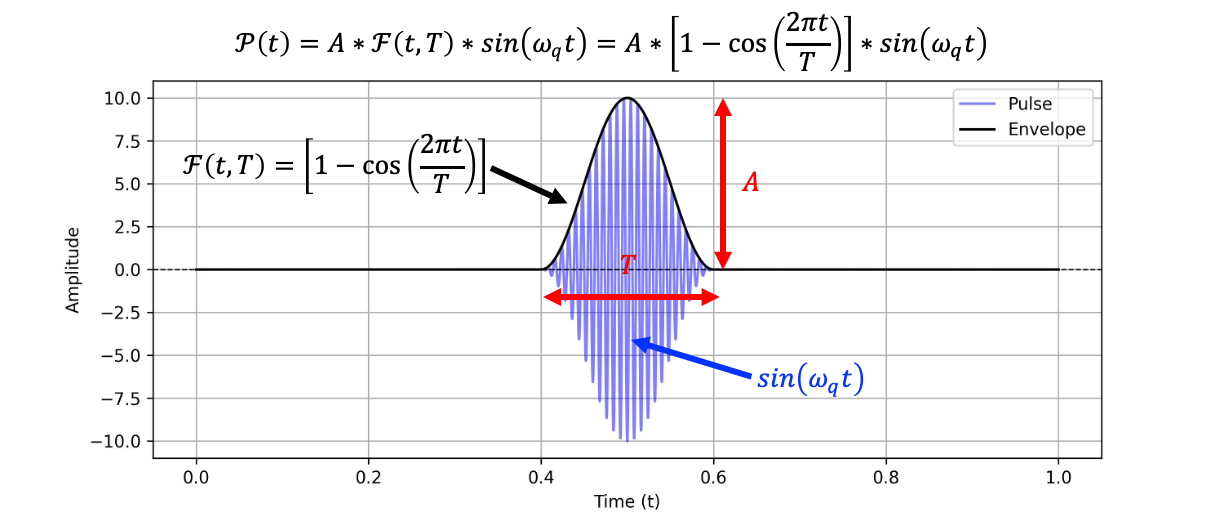
• Pulse Amplitude (\( A \)): Determines the state of the Qubit (the rotation angle on the Bloch sphere)
• Pulse Duration (\( T \)): Determines the state of the Qubit (the rotation angle on the Bloch sphere)
• Pulse Frequency (\( \omega_d \)): Ensures precise driving of the Qubit
• Pulse Envelope (\( F(t, \tau) \)): Affects leakage

A complete pulse can be expressed as: \[ P(t) = A \cdot F(t, \tau) \cdot \sin(\omega_q t) \]

Here’s an example:

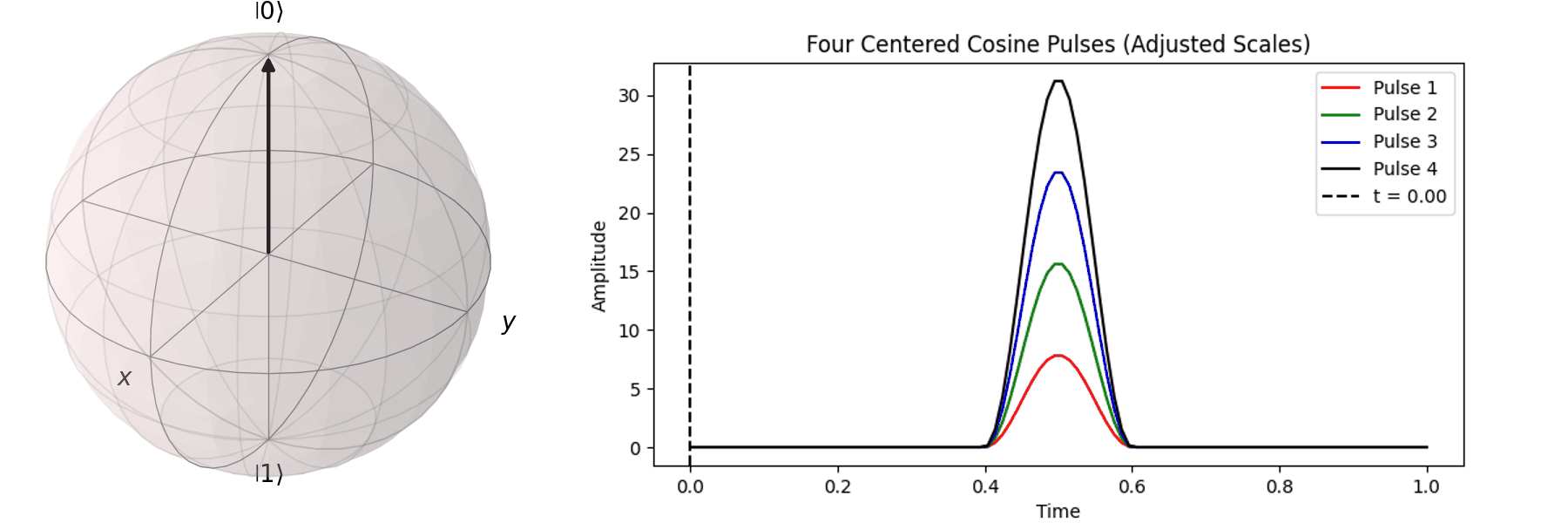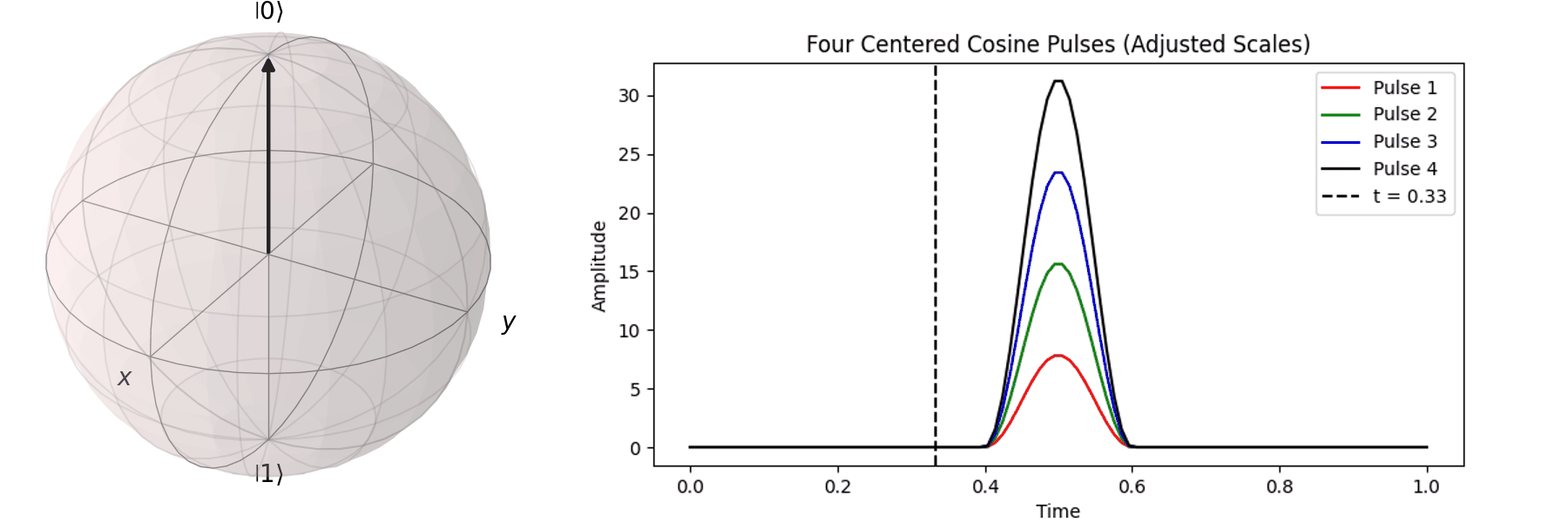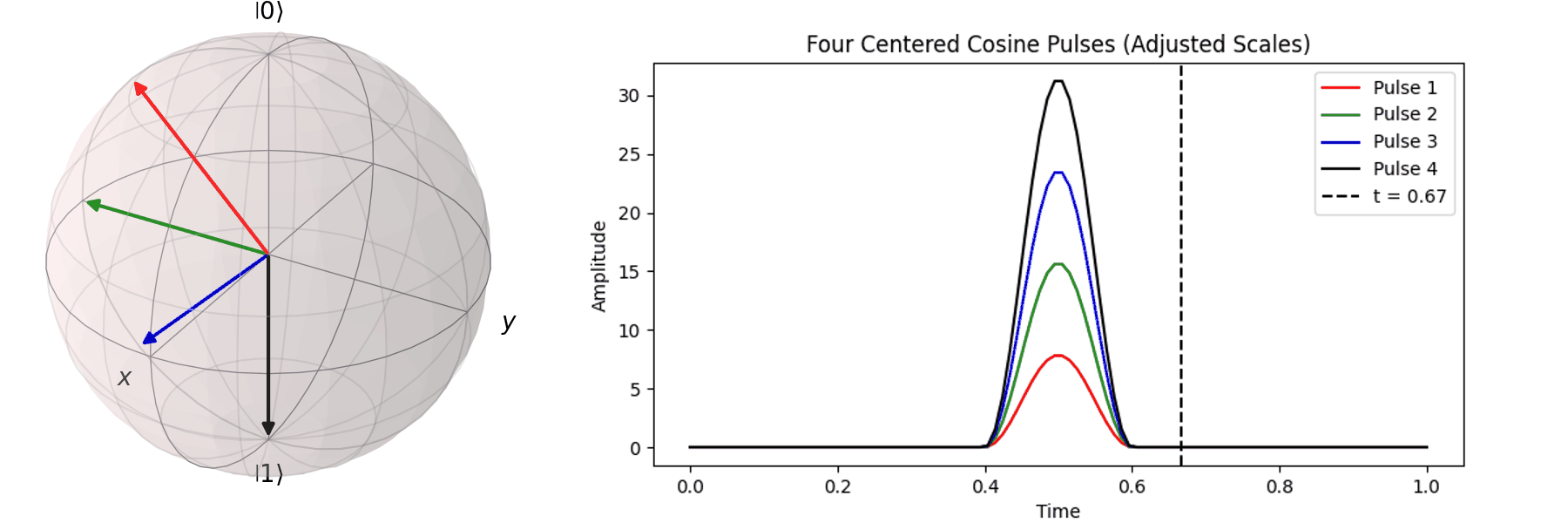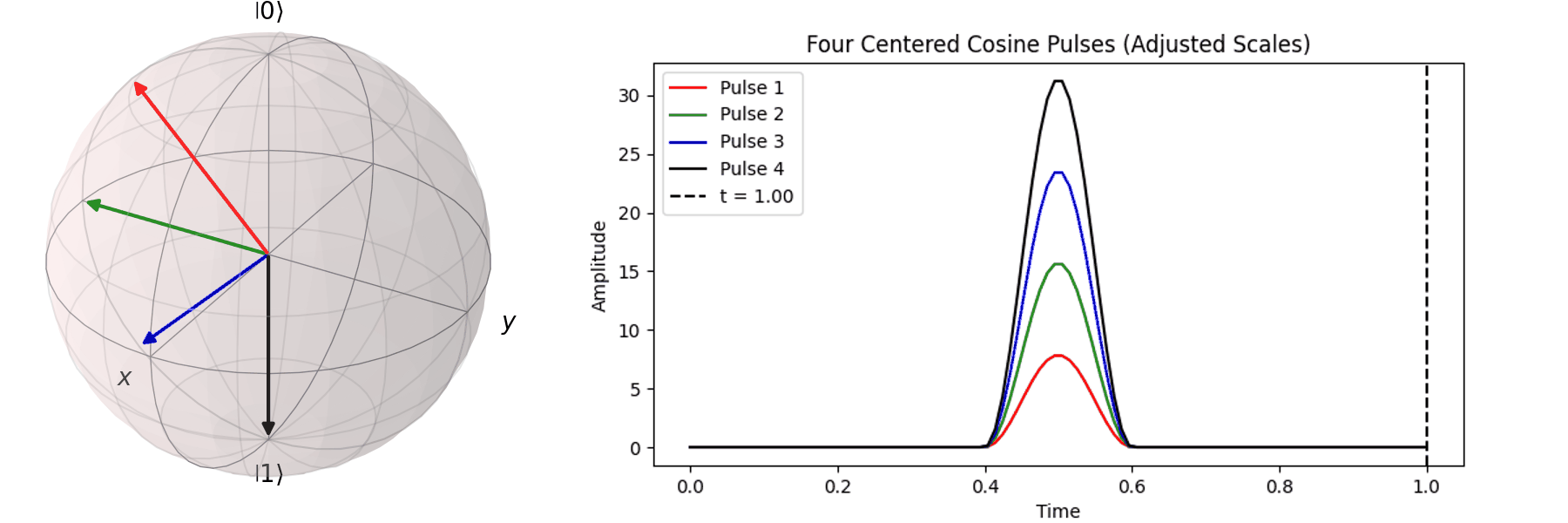
Generally, because the coherence time of a Qubit is very short, we aim to complete Qubit operations as quickly as possible. For superconducting qubits, the coherence time can reach microseconds (\(\mu s\)), which is already considered long in current technology. Therefore, pulses for superconducting qubits are typically in the nanosecond (\(ns\)) range. Consequently, the Qubit state is usually controlled by adjusting the pulse amplitude to determine the rotation angle.
(For example\(^a\), the driving duration is approximately \( 10ns \)). \(^a\): Ref: DOI: 10.1103/PRXQuantum.5.030353

The process can be visualized using the Bloch sphere, as shown here for rotations around the \( X \)-axis by \(0.25\pi\), \(0.5\pi\), \(0.75\pi\), and a full \( \pi \)-pulse. It can be observed that the rotation angle is determined by the pulse amplitude.

Similarly, we can discuss achieving the same \( \pi \)-pulse transition from \( |\ 0\rangle \rightarrow |\ 1\rangle \) using different pulse durations (\( T \)).

Naively, one might think that since superconducting qubits have a short coherence time, the shorter the pulse duration (\( T \)), the better. In the next section, we will discuss how shorter pulses introduce more irrelevant oscillation frequencies, leading to errors in Qubit operations. In practice, determining the appropriate pulse duration (\( T \)) and amplitude (\( A \)) is a crucial part of regular Qubit calibration. Good calibration ensures high-quality quantum computation, whereas poor calibration can result in errors that make quantum computation less accurate than classical computation.

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.