Semiconductor Spin Qubits

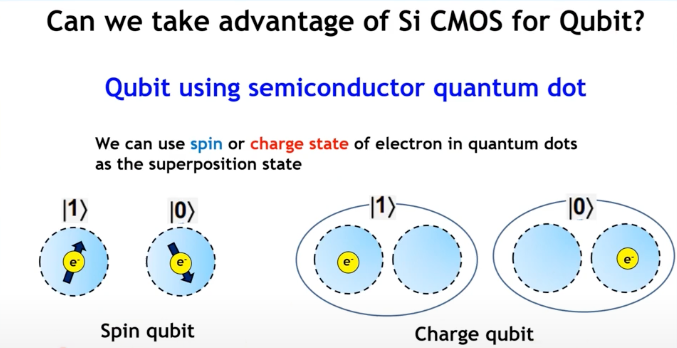
Among the types of semiconductor qubits, the main classification is based on the encoding scheme, i.e., which quantum states are chosen to correspond to \( \ket{0} \) and \( \ket{1} \). They can be encoded using spin (Spin Qubit) or by the number of charges in a quantum dot (Charge Qubit); a single quantum dot can be used, or multiple quantum dots can be combined for encoding. These different encoding schemes involve trade-offs in terms of physical implementation complexity, control methods, and sensitivity to noise.

Spin Qubits and Charge Qubits

▲ As mentioned earlier, semiconductor qubits utilize either intrinsic quantum effects or potential well quantum effects for quantum encoding. A Spin Qubit uses the spin state of an electron in a quantum dot for encoding. In a Charge Qubit, information is encoded by the location of a charge in one of two quantum dots.
Ref: YouTube: [2024 NYCU Electrical Engineering Project Exploration] Prof. Pei-Wen Li Introduction
https://www.youtube.com/watch?v=LuXsf-pWFeI&t=7s

Multi-Quantum Dot Combinations and Types of Spin Encoding

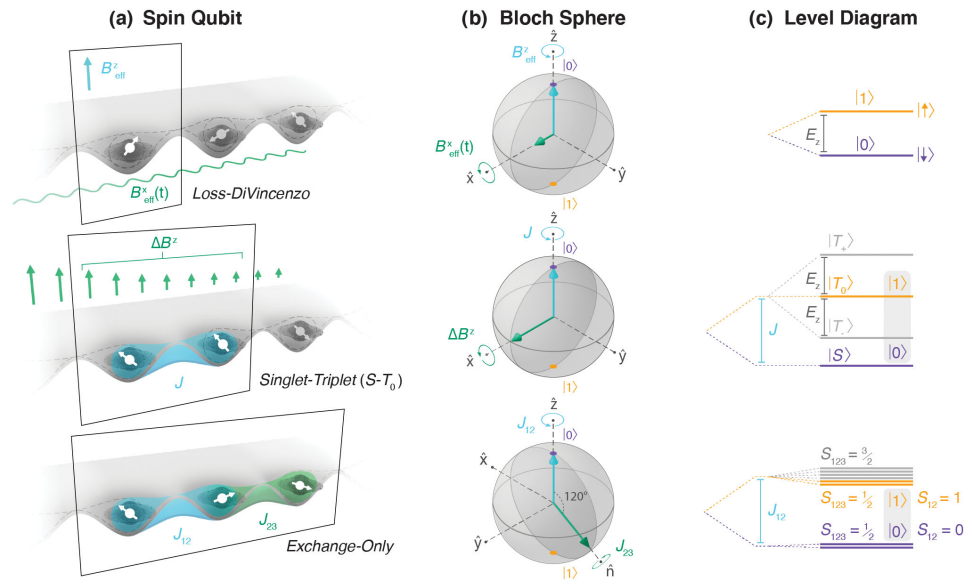
Interestingly, spin qubits can utilize combinations of multiple spins to construct different encoding schemes.

Ref: Semiconductor spin qubits
DOI: 10.1103/RevModPhys.95.025003

• Single-Spin Qubit: This is the most intuitive encoding method. A qubit is encoded in the two states of a single electron confined in a single quantum dot, spin-down \( \ket{0} \) and spin-up \( \ket{1} \), distinguished by applying a z-direction magnetic field \(B_z\). This scheme is conceptually simple and has the most straightforward physical structure. Its control typically requires applying an oscillating magnetic field \(B_x\) resonant with the qubit, i.e., electron spin resonance (ESR), to drive spin rotations. However, generating a precise, localized oscillating magnetic field at the nanoscale is a significant technological challenge, and it only responds to magnetic fields, not electric fields, which has spurred the development of more complex encoding schemes.

• Singlet-Triplet (\(S-T_0\) Qubit): This scheme uses the spins of two electrons in a double quantum dot (DQD) to encode one qubit. Its logical basis states are defined as the 'singlet state' with a total spin of zero, \( \ket{S} = \frac{1}{\sqrt{2}} \left( \ket{\uparrow\downarrow} - \ket{\downarrow\uparrow} \right) \) and the 'triplet state' with a total spin of one and a magnetic quantum number of zero, \( \ket{T_0} = \frac{1}{\sqrt{2}} \left( \ket{\uparrow\downarrow} + \ket{\downarrow\uparrow} \right) \). The advantage of the \(S-T_0\) qubit is that the potential barrier between the two quantum dots can be controlled electrically, thereby turning the overlap of the two electron wave functions on or off, which gives rise to the quantum mechanical effect of exchange interaction. This interaction can directly drive \(Z\)-rotations of the qubit. X-axis rotations, however, require a magnetic field gradient for operation. This method allows the z-axis to be controlled by an electric field and the x-axis by a magnetic field, respectively.

• Exchange-Only Qubit: This is a scheme for all-electrical control, which encodes a logical qubit using three electrons in three quantum dots. By electrically controlling the exchange interaction between adjacent quantum dots, all operations can be performed without any magnetic fields or magnetic field gradients.

The three methods above show a progression from purely magnetic control to all-electrical control by integrating multiple quantum dots, making them easier to integrate into current semiconductor manufacturing processes and control logic. In fact, there are many more rich schemes:

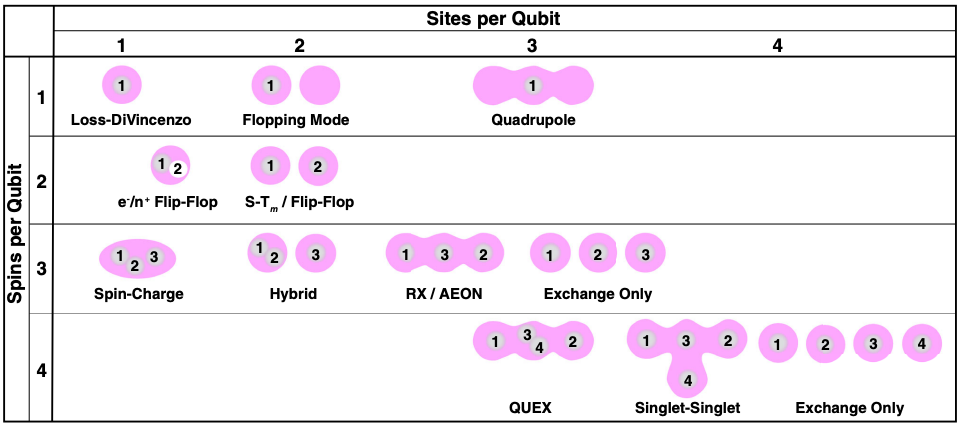
▲ The horizontal axis represents how many quantum dots (pink) a qubit contains, and the vertical axis shows how many spins a qubit contains and in which quantum dots they are distributed.
Ref: Semiconductor spin qubits
DOI: 10.1103/RevModPhys.95.025003

For example, the quantum dot hybrid qubit:

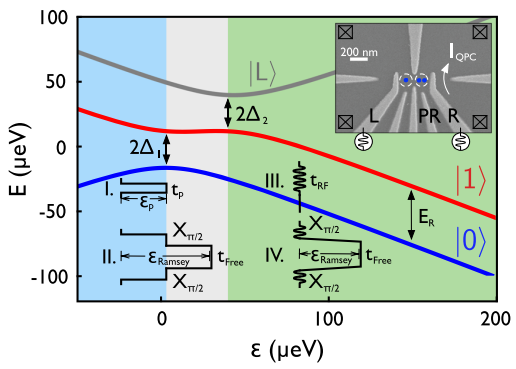
• Quantum Dot Hybrid Qubit: To overcome the reliance of \(S-T_0\) qubits on magnetic field gradients, the hybrid qubit was proposed. It uses three electrons distributed in a double quantum dot (one electron in one dot, two in the other) to encode a qubit. Its logical basis states can be defined as \[ \ket{0} \equiv \ket{\downarrow}\otimes S \] and \[ \ket{1} \equiv \sqrt{\frac{1}{3}}\ket{\uparrow}\otimes T_0-\sqrt{\frac{2}{3}}\ket{\uparrow}\otimes T_{-} \], where \( S \) represents the singlet state in the double-electron dot, and \(T_0, T_{-}\) represent the triplet states. The energy splitting of this encoding is mainly determined by the singlet-triplet energy difference within a quantum dot, thus enabling fast qubit rotations without an external magnetic field gradient, while also being less sensitive to charge noise.

▲ An example of a quantum dot hybrid qubit, showing one and two electrons in the two quantum dots, respectively.
Ref: Extending the coherence of a quantum dot hybrid qubit
DOI: 10.1038/s41534-017-0034-2

The rich variety of quantum dot combinations also corresponds to different quantum state encodings: N represents a qubit containing N quantum dots, q represents the magnetic quantum number. You can compare and see which actual quantum states correspond to \(\ket{0}\) and \(\ket{1}\).

Semiconductor spin qubits
DOI: 10.1103/RevModPhys.95.025003

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.