Semiconductor Spin Qubits

Moving towards quantum computation requires connecting multiple qubits. Semiconductor qubits can be considered "semi-stationary" qubits; because their charge carriers can be moved, they exhibit many rich phenomena. This article introduces the most fundamental characteristics of a double quantum dot.

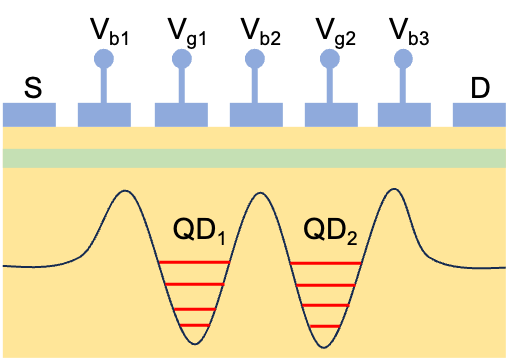
▲ Similar to a single quantum dot, this is a conceptual diagram for defining a double quantum dot. Two quantum dot regions are formed by three barrier gates \(V_{b1}, V_{b2}, V_{b3}\), and the energy levels of the two dots can be tuned by their respective plunger gates \(V_{g1}, V_{g2}\).
Ref: Drawn by the author

Interaction Between Double Quantum Dots

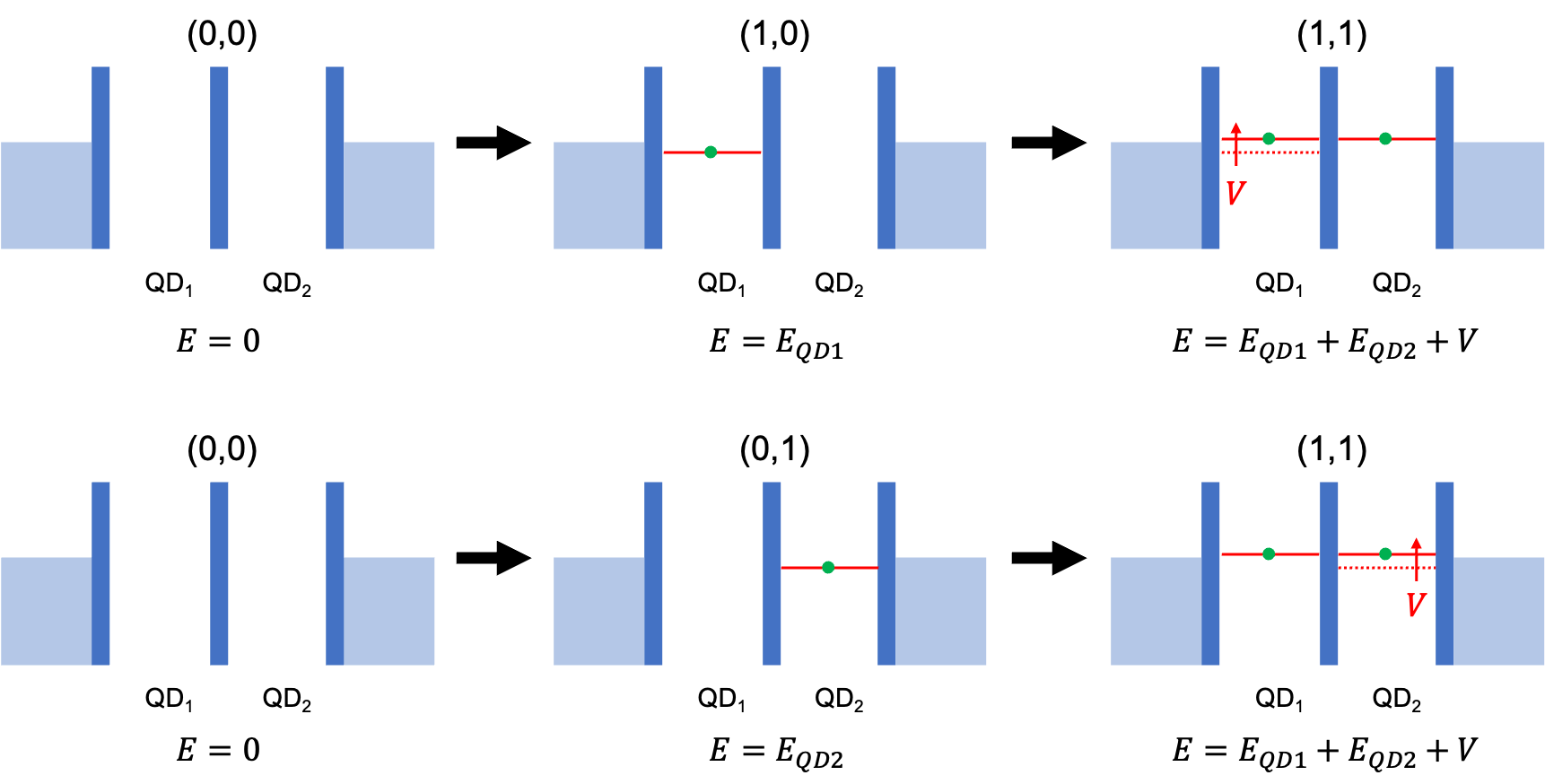
Quantum computation requires interaction between qubits to perform effective quantum information processing. At the microscopic scale, for two closely spaced quantum dots, one must consider the Coulomb interaction between charge carriers and the cross-capacitance between gates. We use the notation \( (N_{QD_1},N_{QD_2})\) to represent the number of charges on the quantum dots \(QD_1\) and \(QD_2\). For example, \((0,1)\) means there are 0 carriers on \(QD_1\) and 1 carrier on \(QD_2\).

▲ Schematic of the Coulomb interaction between carriers in a double quantum dot. When a charge enters one dot, the Coulomb interaction causes the energy level of the other dot to rise.
Ref: Drawn by the author

Measuring Energy Levels & the Stability Diagram

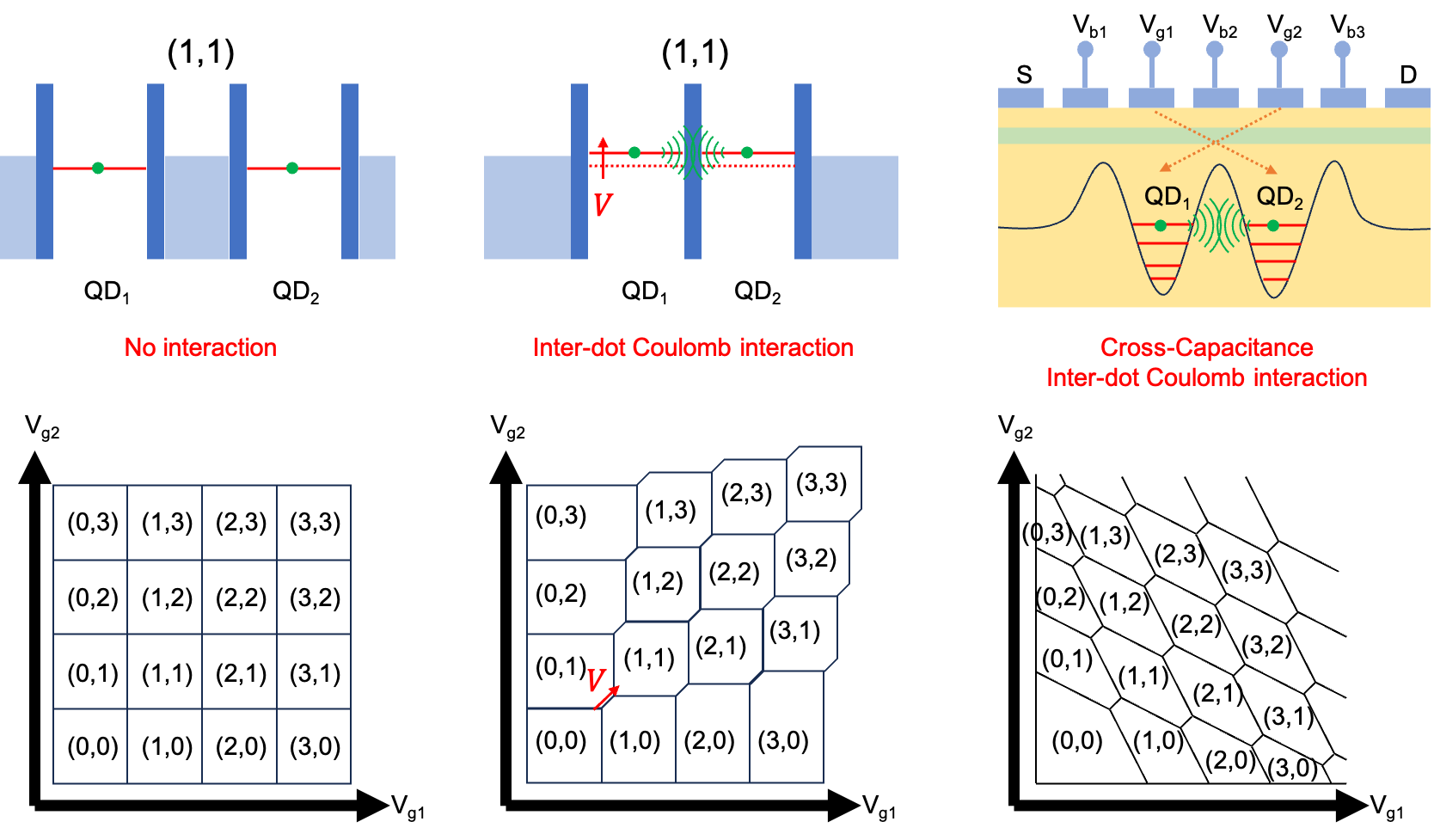
For a single quantum dot, there is the Coulomb Diamond measurement diagram. Similarly, for a double quantum dot, we can measure the energy levels by tuning the gate voltages \(V_{g1}\) and \(V_{g2}\). Due to the close proximity of the two dots, there are Coulomb interactions and capacitive cross-talk between the gates.

▲ (Left) A hypothetical signal diagram for two distant, non-interacting quantum dots, tuned by \(V_{g1}\) and \(V_{g2}\).
(Middle) Considering the Coulomb interaction force between charges.
(Right) The actual characteristics of a double quantum dot. In addition to Coulomb interaction, the cross-talk between the gates causes the characteristic hexagonal shape to appear.
Ref: Drawn by the author

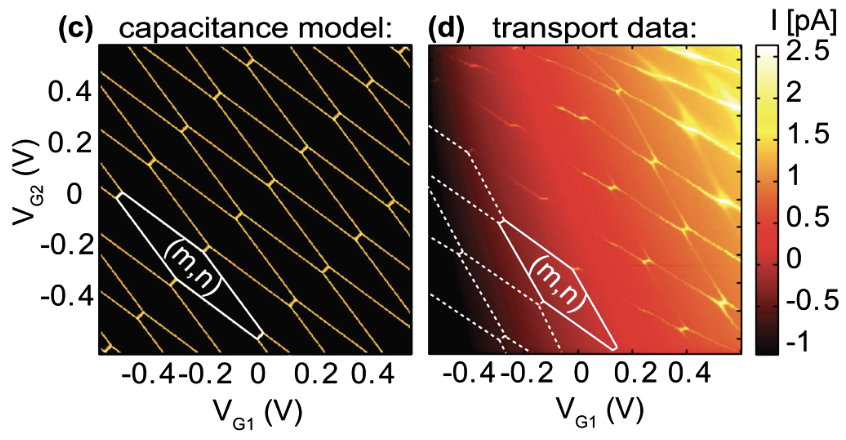
▲ An experimentally measured energy level characteristic plot of a double quantum dot, known as a Stability Diagram.
Ref: Engineering Independent Electrostatic Control of Atomic-Scale (∼4 nm) Silicon Double Quantum Dots
DOI: 10.1021/nl3012903

Carrier Transport Characteristics in a Double Quantum Dot

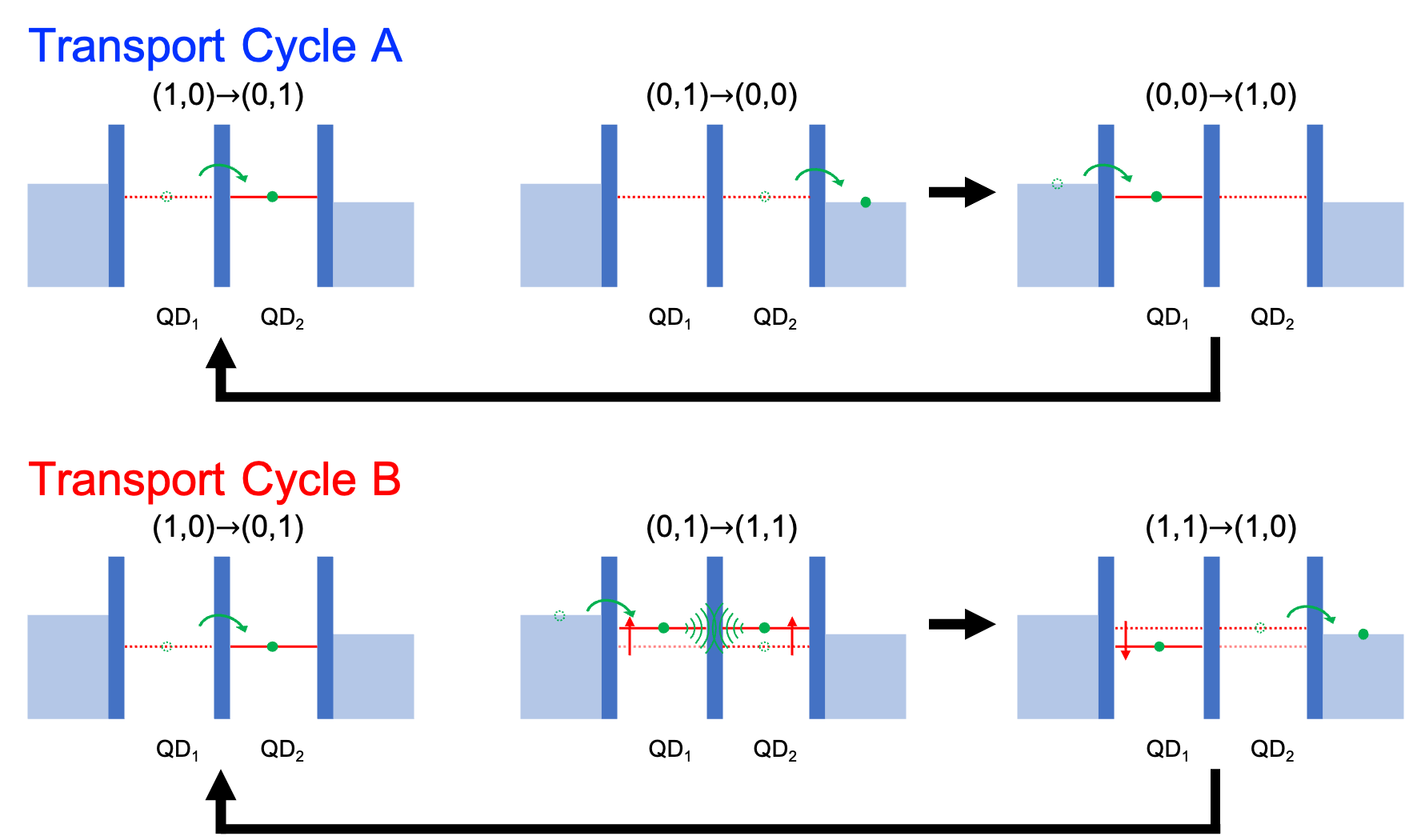
Due to the energy level shifts caused by Coulomb interaction between carriers, the current transport in a double quantum dot can occur through two different processes:

Cycle A is a more intuitive cycle where the energy levels of both quantum dots are aligned within the bias window, naturally forming a step-like flow of carriers.
Cycle B is formed through the interaction between carriers; the addition of a new charge raises an energy level into the bias window, thereby completing a cycle.
Ref: Drawn by the author

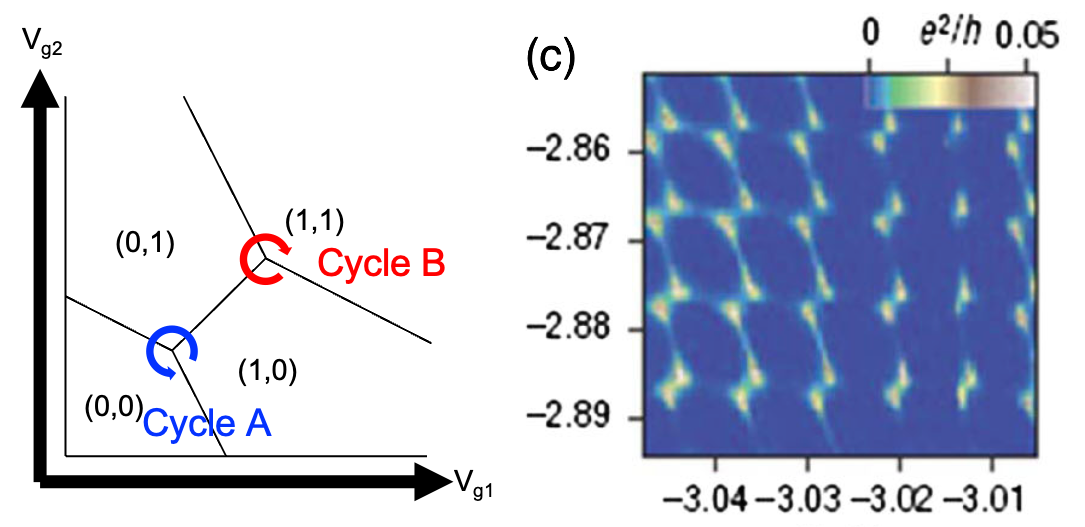
▲ The difference between the two cycles can be understood through the Stability Diagram. Experimentally (right figure), one can also observe that the two different cycles produce pairs of triangular signals (bias triangles).
Ref:
(Left) Drawn by the author
(Right) Silicon quantum electronics, DOI: 10.1103/RevModPhys.85.961

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.