半導體自旋量子位元的種類與編碼方式
在半導體量子位元的種類中,主要的分類方式是依照編碼方式,即選取哪些量子態來對應\( \ket{0} \)與\( \ket{1} \),
可以用自旋方式來編碼(Spin Qubit)、也可以用量子點中帶電數量來編碼(Charge Qubit)
;可以用單個量子點,也可以組合多個量子點來編碼。
這些不同的編碼方案在物理實現的複雜性、操控方式和對雜訊的敏感度上各有取捨。
Spin Qubit與Charge Qubit
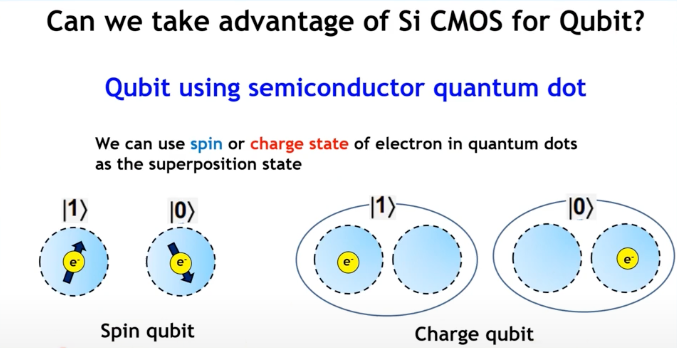
▲前面提到,半導體量子位元就是利用內稟量子效應或位能井量子效應,來進行量子編碼。
Spin Qubit是利用量子點中自旋的狀態來編碼。
而Charge Qubit中,是利用電荷處在兩個量子點之一,來編碼資訊。
Ref: YouTube:【2024陽明交大電機專題探索】李佩雯教授介紹
https://www.youtube.com/watch?v=LuXsf-pWFeI&t=7s
多量子點組合與自旋編碼的種類
有趣的是,自旋量子位元可以利用多個自旋組合,來構造不同的編碼方式。
Ref: Semiconductor spin qubits
DOI: 10.1103/RevModPhys.95.025003
-
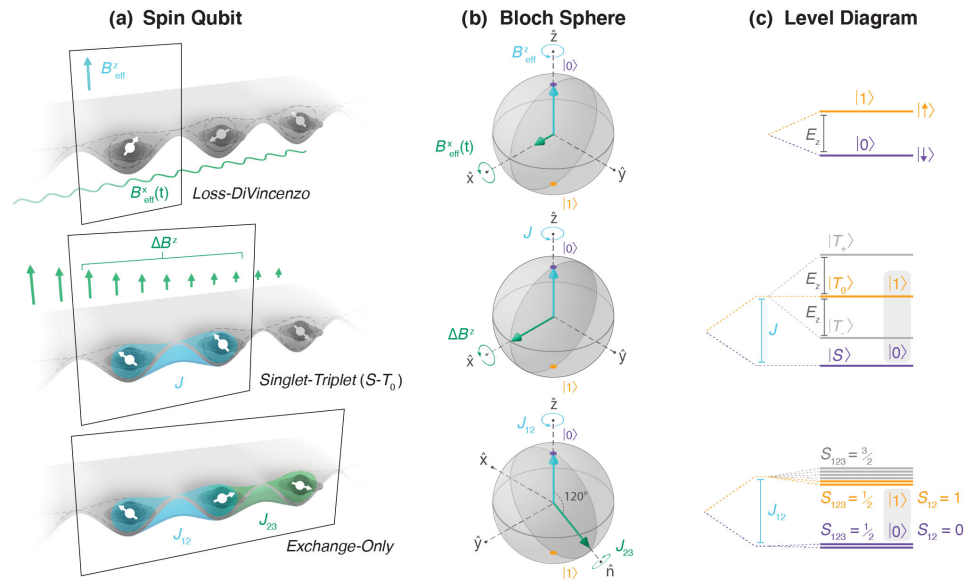
Single-Spin Qubit: 這是最直觀的編碼方式。 一個量子位元被編碼在單一量子點中,施加z方向磁場\(B_z\),來區分電子的自旋向下\(\ket{0}\)和自旋向上\(\ket{1}\)兩個狀態中。 這種方案概念簡單,物理結構也最為簡潔。 其操控通常需要施加一個與量子位元共振的振盪磁場\(B_x\),即電子自旋共振,來驅動自旋的旋轉。 然而,在奈米尺度上產生精確、局域化的振盪磁場是一項重大的技術挑戰,且只對磁場響應,無法用電場來控制,這促使了更複雜編碼方案的發展。
-
Singlet-Triplet (\(S-T_0\) Qubit): 這種方案利用一組雙量子點(Double Quantum Dot, DQD)中的兩個電子的自旋來編碼成一個量子位元。 其邏輯基態被定義為兩個電子的總自旋為0的「單重態」 \( \ket{S} = \frac{1}{\sqrt{2}} \left( \ket{\uparrow\downarrow} - \ket{\downarrow\uparrow} \right) \) 和總自旋為1、磁量子數為0的「三重態」 \( \ket{T_0} = \frac{1}{\sqrt{2}} \left( \ket{\uparrow\downarrow} + \ket{\downarrow\uparrow} \right) \)。 \(S-T_0\)量子位元的優勢在於,可以透過電場方式控制兩個量子點之間的位能高度,從而開啟或關閉兩個電子波函數的交疊,這會產生量子力學效應中的exchange interaction。 這種交互作用可以直接驅動量子位元進行\(Z-Rotation\)。而x軸需要透過磁場梯度來進行操作。 此方式可以讓z軸藉由電場、x軸藉由磁場來個別控制。
-
Exchange-Only Qubit: 這是一種實現全電控的方案,它將一個邏輯量子位元編碼在三個量子點中的三個電子上。透過電場控制相鄰量子點之間的交換交互作用,完全無需任何磁場或磁場梯度來操作。
以上三種的方式,利用整合多個量子點的方式,逐步將純磁場控制改良成全電場的控制,便於整合進當前的半導體製程與控制邏輯中。 事實上,還有更多豐富的方案:
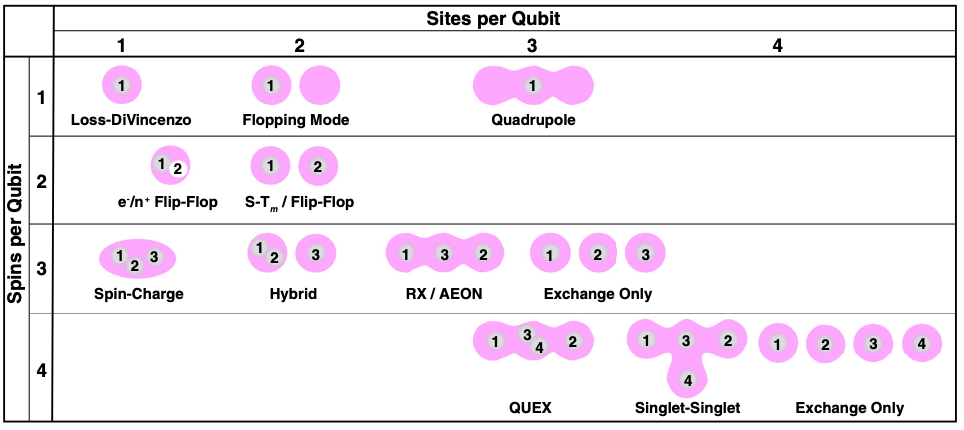
▲橫向表示一個量子位元包含幾個量子點(粉色)、縱向表示一個量子位元包含幾個自旋並分布在哪個量子點中。
Ref: Semiconductor spin qubits
DOI: 10.1103/RevModPhys.95.025003
舉例像是量子點混合量子位元:
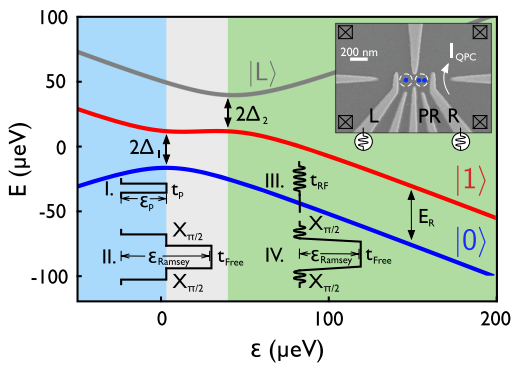
量子點混合量子位元 (Quantum Dot Hybrid Qubit): 為了克服 \(S-T_0\) 量子位元對磁場梯度的依賴,進一步提出混合量子位元。 它利用三個電子 分佈在一個雙量子點中(一個點有一個電子,另一個點有兩個)來編碼量子位元。 其邏輯基態可以被定義為 \[ \ket{0} \equiv \ket{\downarrow}\otimes S \] 和 \[ \ket{1} \equiv \sqrt{\frac{1}{3}}\ket{\uparrow}\otimes T_0-\sqrt{\frac{2}{3}}\ket{\uparrow}\otimes T_{-} \], 其中 \( S \) 代表雙電子點中的單重態、\(T_0, T_{-}\)代表雙電子點中的三重態。 這種編碼的能階分裂主要由量子點內的單重態–三重態能量差決定,因此不需要外部磁場梯度就能實現快速的量子位元旋轉,同時對電荷雜訊也較不敏感。
▲量子點混合量子位元的例子,可以看出兩個量子點中分別帶有一個與兩個電子。
Ref: Extending the coherence of a quantum dot hybrid qubit
DOI: 10.1038/s41534-017-0034-2
而豐富的量子點組合方式,也有不同的量子態編碼與之對應:N表示一個量子位元含有N個量子點、q代表磁量子數,可以比對\(\ket{0},\ket{1}\)對應到的實際量子態為何?
Semiconductor spin qubits
DOI: 10.1103/RevModPhys.95.025003

 王培儒
王培儒