隱藏子群問題

用時空來理解隱藏子群問題：旋轉、平移

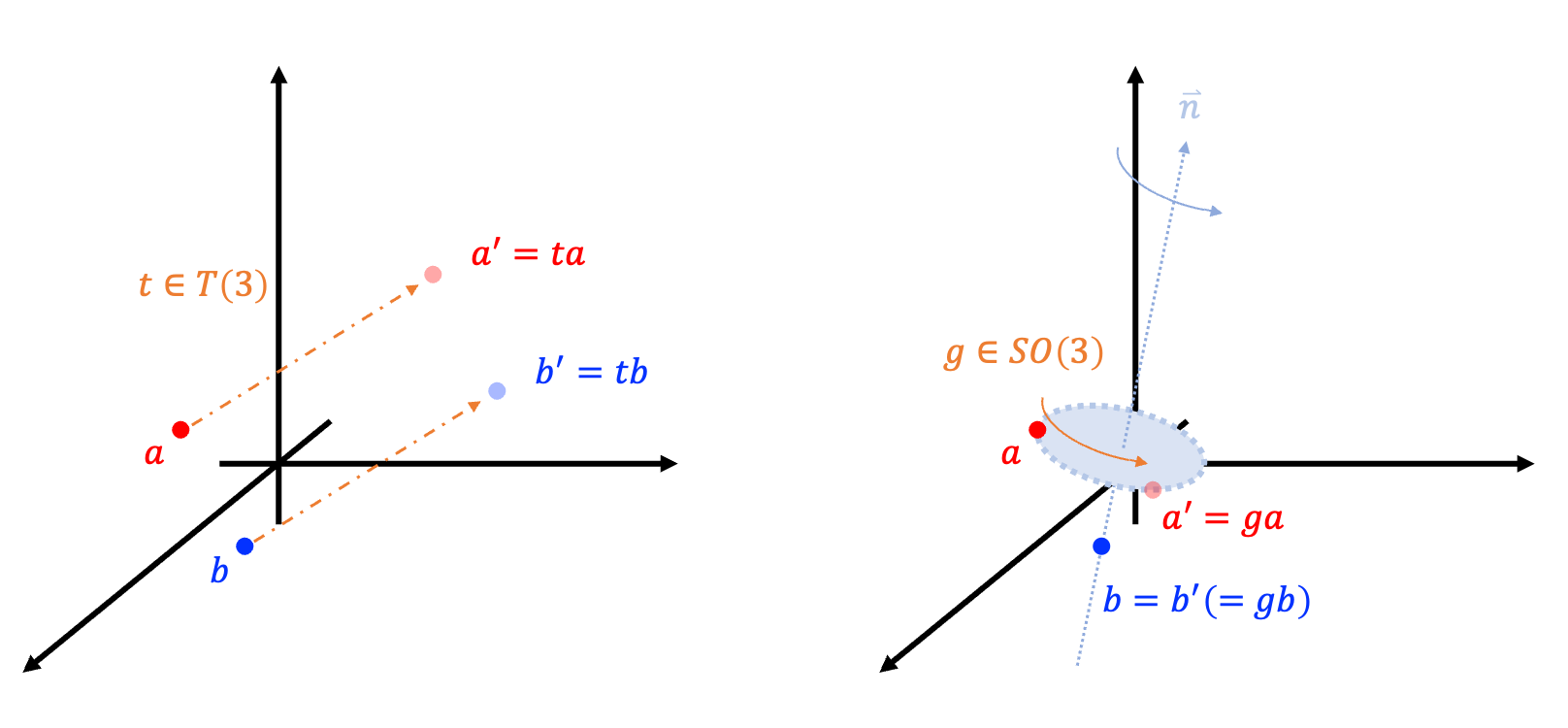
時空\(M\)是日常每個人都會經驗到的事物，最適合用來解釋隱藏子群的概念。 生活中的「移動」，可以分成旋轉、和平移。 可以迅速的理解是，旋轉會構成旋轉群\(SO(n)\)(轉10度、再轉20度等於轉30度)、平移構成平移群\(T(n)\)(向前2公尺、再向後4公尺，等於向後2公尺)，我們統稱旋轉群+平移群為歐幾里得群\(E(n)\)。 \(n\)是時空的維度，只討論空間的話就是\(3\)。

理論上，通過歐幾里得群\(E(n)\)，我們可以位移到宇宙的任何一個地方，數學上，我們稱歐幾里得群\(E(n)\)對時空的作用是「傳遞的」（Transitive）， 即對任何\(x,y\)是時空的兩點，都存在\(g\in E(n)\)使得\(y＝g*x\)。或是說，給定原點\(x_0\)，\(E(n)*x_0\)就是全宇宙\(M\)。

▲ 三維世界裡的平移\(T(3)\)（左）與旋轉\(SO(3)\)（右）。繞軸\(\vec{n}\)旋轉時，軸線上的點並不會被移動。

穩定子(Stabilizer)

聰明的讀者其實可以發現，我們只需要平移群\(T(n)\)，就可以到達全宇宙；而且，旋轉存在不動點（fixed point），即對旋轉的圓心\(x_c\)，無論怎麼旋轉，都還是同一點\(E(n)*x_c=x_c\)。 這就導致了旋轉與平移最大的差異：旋轉有不動點，但平移沒有。 具有不動點構成子群\(SO(n)\subset E(n)\)，稱為穩定子（Stabilizer），而整個時空\(M \cong E(n)/SO(n)\)，時空可以視為歐幾里得群\(E(n)\)對子群\(SO(n)\)陪集空間！ 這就是克萊因幾何：如果群\(G\)作用在一個幾何\(M\)是Transitive，而群作用如果有不動點子群（穩定子，\(H\)），則整個幾何\(M\cong G/H\)是陪集空間。

本文部分內容經由 AI 工具協助生成與編輯，經作者審核。